二维前缀和,二维差分,离散化技巧
二维前缀和
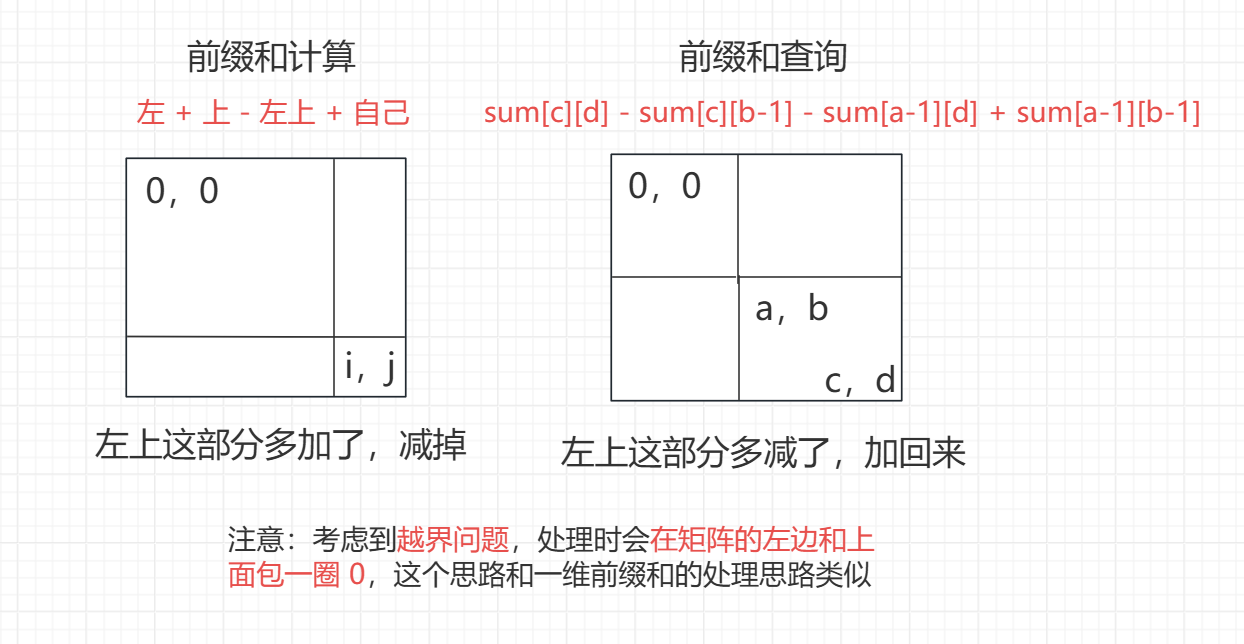
原理解析
模板题目
https://leetcode.cn/problems/range-sum-query-2d-immutable/
代码实现
java
class NumMatrix {
public int[][] sum;
public NumMatrix(int[][] matrix) {
int n = matrix.length;
int m = matrix[0].length;
// 防止越界,在矩阵的左边和上方包一圈 0
sum = new int[n + 1][m + 1];
for (int a = 1, c = 0; c < n; a++, c++) {
for (int b = 1, d = 0; d < m; b++, d++) {
// 平移处理
// 原来的 i,j 位置的值拷贝到 i+1,j+1 位置
sum[a][b] = matrix[c][d];
}
}
// 计算前缀和
// 包了 0,起始位置为 1,1 开始计算
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// 左 + 上 - 左上 + 自己
sum[i][j] += sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];
}
}
}
// 原来是 row 1,col 1, row 2,col 2,这里改成 a,b,c,d
public int sumRegion(int a, int b, int c, int d) {
// 平移前的前缀和查询公式
// sum[c][d] - sum[c][b-1] - sum[a-1][d] + sum[a-1][b-1]
// 因为实在平移后的矩阵中算前缀和,所以 c++,d++
// 因为在原始前缀和查询公式中 a,b 都会减一,又因为是平移处理的
// 所以 a,b 不用平移,天然的表示减一位置
// 简单理解:因为要平移,所以对原始前缀和查询公式所有位置 +1 处理
c++;
d++;
return sum[c][d] - sum[c][b] - sum[a][d] + sum[a][b];
}
// public int sumRegion(int a, int b, int c, int d) {
// a++;
// b++;
// c++;
// d++;
// return sum[c][d] - sum[c][b-1] - sum[a-1][d] + sum[a-1][b-1];
// }
}
/**
* Your NumMatrix object will be instantiated and called as such:
* NumMatrix obj = new NumMatrix(matrix);
* int param_1 = obj.sumRegion(row1,col1,row2,col2);
*/边框都是 1 的最大正方形
题目链接
https://leetcode.cn/problems/largest-1-bordered-square/
思路分析
时间复杂度:O(m * n * min(m,n)),m,n 表示所左上角点的可能位置,min(m,n)表示正方形边长的可能性
如果确定每个正方形后再去遍历边长判断是否都为 1,则复杂度还要再原基础上再 * 4 * min(m,n),而本题优化的点就是在判断这里能不能更快
判断周长是否全为 1,可以用外围的面积减去内部的面积,如果面积差值 = 4 * 边长,那就是合法的正方形,计算面积的过程可以使用二位前缀和实现
只关心每个位置的二维前缀和,用于计算面积进而判断是否合法,原数组并不关心,所以可以复用原数组,将其转为二维前缀和数组,复用后无法补 0,注意边界条件的判断,复用了原数组还节省了空间
空间复杂度:O(1)
代码实现
java
class Solution {
public int largest1BorderedSquare(int[][] grid) {
int n = grid.length;
int m = grid[0].length;
build(n, m, grid);
// 特判:如果前缀和都为 0,压根就没有 1
if (sum(grid, 0, 0, n - 1, m - 1) == 0) {
return 0;
}
// 1 * 1 的正方形肯定存在,找更大的正方形
int ans = 1;
// 枚举所有可能的左上角顶点
for (int a = 0; a < n; a++) {
for (int b = 0; b < m; b++) {
// 左上角顶点 (a,b),右下角顶点 (c,d),枚举可能的边长
// +ans 表示剪枝,在原来相对大的正方形的基础上找更大的
// 不要重复遍历已经遍历过的部分,边长 k 从 ans + 1 开始
for (int c = a + ans, d = b + ans, k = ans + 1; c < n && d < m; c++, d++, k++) {
// 找到了更大的正方形边长,更新答案
// 外层大正方形边长为 k,内层正方形的周长:(k - 1) * 2
if (sum(grid, a, b, c, d) - sum(grid, a + 1, b + 1, c - 1, d - 1) == (k - 1) << 2) {
ans = k;
}
}
}
}
return ans * ans;
}
// 将原始数组 g 变成前缀和数组,复用自己
// 注意这里无法补 0,需要注意边界判断
// 计算二维前缀和:左 + 上 - 左上 + 自己
public static void build(int n, int m, int[][] g) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
g[i][j] += get(g, i, j - 1) + get(g, i - 1, j) - get(g, i - 1, j - 1);
}
}
}
// 二维前缀和查询,左上角顶点 (a,b),右下角顶点 (c,d)
public static int sum(int[][] g, int a, int b, int c, int d) {
// 加上特判,例如只有 2 * 2 的正方形,就没有内部空间,但是计算后 a,c 错位了
return a > c ? 0 : (g[c][d] - get(g, c, b - 1) - get(g, a - 1, d) + get(g, a - 1, b - 1));
}
// 由于无法补 0,写一个方法处理越界情况
public static int get(int[][] g, int i, int j) {
return (i < 0 || j < 0) ? 0 : g[i][j];
}
}二维差分
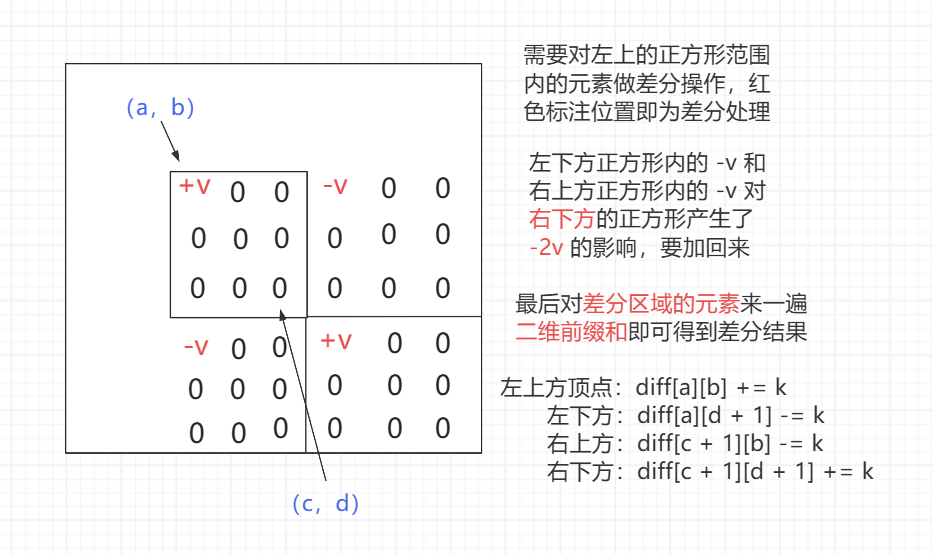
原理分析
⚠️ 注意:会在矩阵外层包一圈 0,可以避免很多边界的讨论
模板题目
https://www.luogu.com.cn/problem/P3397
代码实现
java
import java.io.*;
public class Main {
// 外围会包一层 0 ,避免了很多边界处理
// 对于行和列都多出了 2 行(列),所以要加 2
public static int MAXN = 1002;
public static int[][] diff = new int[MAXN][MAXN];
public static int n, q;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken() != StreamTokenizer.TT_EOF) {
n = (int) in.nval;
in.nextToken();
q = (int) in.nval;
for (int i = 1, a, b, c, d; i <= q; i++) {
in.nextToken();
a = (int) in.nval;
in.nextToken();
b = (int) in.nval;
in.nextToken();
c = (int) in.nval;
in.nextToken();
d = (int) in.nval;
add(a, b, c, d, 1);
}
build();
for (int i = 1; i <= n; i++) {
out.print(diff[i][1]);
for (int j = 2; j <= n; j++) {
out.print(" " + diff[i][j]);
}
out.println();
}
clear();
}
out.flush();
out.close();
br.close();
}
// 差分处理
public static void add(int a, int b, int c, int d, int k) {
diff[a][b] += k;
// 右上方
diff[c + 1][b] -= k;
// 左下方
diff[a][d + 1] -= k;
// 右下方
diff[c + 1][d + 1] += k;
}
// 加工前缀和
public static void build() {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
// 左 + 上 - 左上 + 自己
diff[i][j] += diff[i][j - 1] + diff[i - 1][j] - diff[i - 1][j - 1];
}
}
}
// 采用静态空间,清理脏数据,不影响下一组测试用例
public static void clear() {
for (int i = 1; i <= n + 1; i++) {
for (int j = 1; j <= n + 1; j++) {
diff[i][j] = 0;
}
}
}
}二维前缀和 + 差分
题目链接
https://leetcode.cn/problems/stamping-the-grid/
思路分析
1 表示不能贴邮票的区域,0 表示可以贴邮票的区域
遍历每一个 0,来到一个 0 位置判断能不能贴
二维前缀和:当前 0 位置开始找出邮票大小的区域,如果前缀和 > 0,说明该区域有 0,不能贴邮票
二维差分:贴了邮票,该区域就不能贴邮票了,利用差分将该区域都修改为 1
如果原始数组中 0 位置的元素在差分数组中对应位置的值是 1,说明 0 位置贴贴上了邮票,否则就没有贴上邮票
最后判断原始矩阵和差分矩阵中对应位置的元素是不是 0,如果是 0,说明没有贴上邮票,返回 false
代码实现
java
class Solution {
// 时间复杂度O(n*m),额外空间复杂度O(n*m)
// 原来是 int stampHeight, int stampWidth,这里改成 int h, int w
public boolean possibleToStamp(int[][] grid, int h, int w) {
int n = grid.length;
int m = grid[0].length;
// sum 是前缀和数组,左边和上面包一层 0,避免边界讨论
int[][] sum = new int[n + 1][m + 1];
// 将原始数组的内容拷贝到 sum 数组中,再做前缀和处理
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
sum[i + 1][j + 1] = grid[i][j];
}
}
// 加工前缀和,得到前缀和数组的结果
build(sum);
// diff 是差分数组,外层包一圈 0,避免边界讨论
// 当贴邮票的时候,不在原始矩阵里贴,在差分矩阵里贴
// 原始矩阵就用来判断能不能贴邮票,不进行修改
// 每贴一张邮票都在差分矩阵里修改
int[][] diff = new int[n + 2][m + 2];
for (int a = 1, c = a + h - 1; c <= n; a++, c++) {
for (int b = 1, d = b + w - 1; d <= m; b++, d++) {
if (sumRegion(sum, a, b, c, d) == 0) {
// 原始矩阵中 (a,b)左上角点
// 根据邮票规格,h、w,算出右下角点(c,d)
// 如果这个区域的元素都是 0 ,则说明
// sumRegion(sum, a, b, c, d) == 0
// 那么此时这个区域可以贴邮票
add(diff, a, b, c, d);
}
}
}
// 加工前缀和,得到差分数组的结果
build(diff);
// 检查所有的格子,如果原始数组和差分数组中对应位置的元素为 0
// 说明不能贴邮票,不符合题意,返回 false
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
// diff 数组是包了一层 0 的,注意平移关系
if (grid[i][j] == 0 && diff[i + 1][j + 1] == 0) {
return false;
}
}
}
return true;
}
// 加工前缀和
public void build(int[][] m) {
for (int i = 1; i < m.length; i++) {
for (int j = 1; j < m[0].length; j++) {
// 左 + 上 - 左上 + 自己
m[i][j] += m[i - 1][j] + m[i][j - 1] - m[i - 1][j - 1];
}
}
}
// 前缀和查询
public int sumRegion(int[][] sum, int a, int b, int c, int d) {
return sum[c][d] - sum[c][b - 1] - sum[a - 1][d] + sum[a - 1][b - 1];
}
// 差分处理
public void add(int[][] diff, int a, int b, int c, int d) {
// 左上方
diff[a][b] += 1;
// 右下方
diff[c + 1][d + 1] += 1;
// 左下方
diff[c + 1][b] -= 1;
// 右上方
diff[a][d + 1] -= 1;
}
}离散化技巧
原理分析
(1)当边长出现小数,负数,无法转换为数组下标的时候,可以等比例缩放边长
对于本题,用左右上下表示力场的边界,r 表示力场的边长,(x,y)为力场的中心点坐标
则 X 左 = 2 * x - r,X 右 = 2 * x + r,Y 下 = 2 * y - r,Y 上 = 2 * y + r
(2)当数值的范围很大时,然而题目只关心种类的数量,可以忽略原始的真实大小,关注数量,使用离散化数组压缩存储,排序 + 去重实现,重新编号,每个数值对应一个编号
例如 x 为 120,去重排序后找到 120 对应的数组索引下标,编号 = 下标索引 + 1,计算 120 对应的编号,则后续再出现 120 的时候,就认为 120 对应的编号表示 120 这个位置,而不用根据真实的值开辟空间
原因:(1)如果数值很大,数据需要开辟的空间也很大(2)如果数组中有很多重复的元素,就浪费了很多空间,使用同一个编号就可以表示多个相同的值,同时编号远远比元素的真实值小的多,这样就大大的节省了空间
题目链接
https://leetcode.cn/problems/xepqZ5/
思路分析
本题的叠加力场就是铺地毯场景,即对每一个力场做差分处理,只要有力场存在,则该力场范围内的元素全部加一,最后遍历所有格子,找出最大的格子的值,这就是叠加力场的值
本题有两个点需要离散化处理,一是顶点坐标可能出现小数,二是每个力场中心点坐标和边长会很大,根据题目数据,可以达到 109,显然不可能开辟这么大的内存空间,不关注力场的实际大小,只关注力场的个数,维持相对位置关系即可,相当于等比例缩放
代码实现
java
class Solution {
// 原来这里是 forceField,这里改成 fields
// 时间复杂度O(n^2),额外空间复杂度O(n^2),n是力场的个数
public int fieldOfGreatestBlessing(int[][] fields) {
int n = fields.length;
// n :矩阵的个数,一个力场带来两个边界
long[] xs = new long[n << 1];
long[] ys = new long[n << 1];
// 离散化处理 1,等比例缩放,去除小数的影响
for (int i = 0, k = 0, p = 0; i < n; i++) {
// x,y 中心坐标,r 正方形的边长
long x = fields[i][0];
long y = fields[i][1];
long r = fields[i][2];
// 左边界
xs[k++] = (x << 1) - r;
// 右边界
xs[k++] = (x << 1) + r;
// 下边界
ys[p++] = (y << 1) - r;
// 上边界
ys[p++] = (y << 1) + r;
}
// 离散化处理 2,排序 + 去重,压缩存储
// xs数组中,排序了且相同值只留一份,返回有效长度,ys 同理
int sizex = sort(xs);
int sizey = sort(ys);
// 差分数组,外层包了一圈 0,避免边界讨论
// n 个力场,sizex:2 * n,sizey:2 * n
int[][] diff = new int[sizex + 2][sizey + 2];
for (int i = 0, a, b, c, d; i < n; i++) {
long x = fields[i][0];
long y = fields[i][1];
long r = fields[i][2];
// 这里不再用真实值,而是用其对应的编号,达到节省空间的目的
a = rank(xs, (x << 1) - r, sizex);
b = rank(ys, (y << 1) - r, sizey);
c = rank(xs, (x << 1) + r, sizex);
d = rank(ys, (y << 1) + r, sizey);
add(diff, a, b, c, d);
}
int ans = 0;
for (int i = 1; i < diff.length; i++) {
for (int j = 1; j < diff[0].length; j++) {
// 加工前缀和:左 + 上 - 左上 + 自己
// 加工前缀和的同时同步更新最大力场强度
diff[i][j] += diff[i - 1][j] + diff[i][j - 1] - diff[i - 1][j - 1];
ans = Math.max(ans, diff[i][j]);
}
}
return ans;
}
// nums 有序数组,有效长度为 size,且 0 ~ size-1 范围上无重复值
// 已知 v 一定在 nums[0 ~ size -1] 上,返回 v 所对应的编号
// 使用二分查找实现,优化时间复杂度
public int rank(long[] nums, long v, int size) {
int l = 0;
int r = size - 1;
int ans = 0;
while (l <= r) {
int mid = (l + r) / 2;
if (nums[mid] >= v) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
// 注意:返回的是编号,ans 是索引下标
return ans + 1;
}
// 排序 + 去重,返回有效元素的个数,size 控制
// 返回数组中有效元素的个数
public int sort(long[] nums) {
Arrays.sort(nums);
int size = 1;
for (int i = 1; i < nums.length; i++) {
// 不相等就填过来,相同就跳过
if (nums[i] != nums[size - 1]) {
nums[size++] = nums[i];
}
}
return size;
}
// 二维差分
public void add(int[][] diff, int a, int b, int c, int d) {
// 左上方
diff[a][b] += 1;
// 右上方
diff[c + 1][b] -= 1;
// 左下方
diff[a][d + 1] -= 1;
// 右下方
diff[c + 1][d + 1] += 1;
}
}