马踏棋盘算法
游戏连接
https://h5.17173.com/content/05252016/143559215.shtml
基本介绍
马踏棋盘算法又称为骑士周游问题
游戏规则
只能走日字,棋盘上的每一个点都需要走一遍才算成功
相关考点
图的深度遍历
回溯思想
贪心思想优化
类补充
Point 类,它是 Java AWT(Abstract Window Toolkit)库中的一个基础类,用于表示二维坐标系中的点
包含两个属性:x:点的 X 坐标(水平位置);y:点的 Y 坐标(垂直位置)
思路分析
1. 创建棋盘
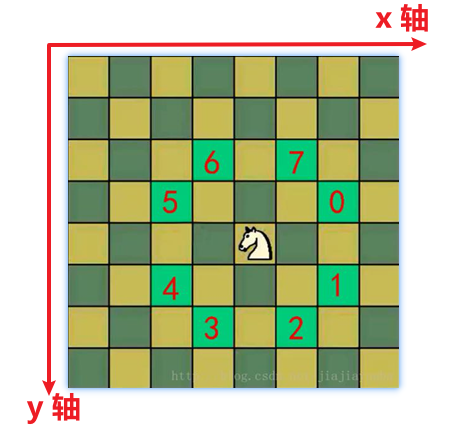
chessBoard,是二维数组 2. 将当前位置设置为已经访问,然后根据当前位置,计算马儿还能走哪些位置,并放入到一个集合中 (
ArrayList),最多有 8 个,每走一步,使用step + 13. 遍历
ArrayList中存放的所有位置,看看那个可以走,如果可以走通,就继续;走不通,就回溯 4. 判断马儿是否完成了任务,使用
step和应该走的步数比较,如果没有达到数量,则表示没有完成任务,将整个棋盘设置为 0
注意:马儿走的策略不同,则得到的结果也不一样,效率也不一样。
代码实现
java
import java.awt.*;
import java.util.ArrayList;
public class HorseChessBoard {
// 初始化属性
// 棋盘大小
private static int X = 6;
private static int Y = 6;
// 棋盘
private static int[][] chessBoard = new int[Y][X];
// 是否访问过,用数组记录
private static boolean vistited[] = new boolean[X * Y];
// 记录是否遍历完棋盘
private static boolean finished = false;
// 主函数:测试
public static void main(String[] args) {
// 初始位置(坐标)
int row = 6;
int col = 1;
// 测试
long start = System.currentTimeMillis();
// 需要传入数组下标,因为是二维矩阵
traversalChessBoard(chessBoard, row - 1, col - 1, 1);
long end = System.currentTimeMillis();
System.out.println("执行耗时:" + (end - start));
// 打印结果
for (int[] rows : chessBoard) {
for (int val : rows) {
System.out.print(val + "\t");
}
System.out.println();
}
}
// 核心代码,遍历棋盘
public static void traversalChessBoard(int[][] chessBoard, int row, int col, int step) {
// 把 step 记录到 chessBoard 中
chessBoard[row][col] = step;
// 设置该位置已经访问过(位置下标由二维矩阵推算)
vistited[row * X + col] = true;
// 获取从当前位置开始,下一个可以走的位置有哪些
ArrayList<Point> points = next(new Point(col, row)); // 主函数传入的起始坐标
// 遍历
while (!points.isEmpty()) {
// 取集合中的第一个点
Point p = points.remove(0);
// 判断是否走过
if (!vistited[p.y * X + p.x]) {
// 递归遍历(先传行再传列)
traversalChessBoard(chessBoard, p.y, p.x, step + 1);
}
}
// 遍历结束,判断是否走完棋盘,如果没有遍历成功就重置,然后回溯
if (step < X * Y && !finished) {
chessBoard[row][col] = 0;
vistited[row * X + col] = false;
} else {
finished = true;
}
}
// 创建ArrayList,用来存储可以走的位置(加入判断逻辑,该位置是否合理)
public static ArrayList<Point> next(Point curPoint) {
// 创建ArrayList
ArrayList<Point> points = new ArrayList<>();
// 创建 Point 对象
Point point = new Point();
//判断在 curPoint 是否可以走如下位置,如果可以走,就将该点(Point) 放入到points
//判断是否可以走5位置
if ((point.x = curPoint.x - 2) >= 0 && (point.y = curPoint.y - 1) >= 0) {
points.add(new Point(point)); //这里一定要new Point
}
//判断是否可以走6位置
if ((point.x = curPoint.x - 1) >= 0 && (point.y = curPoint.y - 2) >= 0) {
points.add(new Point(point)); //这里一定要new Point
}
//判断是否可以走7位置
if ((point.x = curPoint.x + 1) < X && (point.y = curPoint.y - 2) >= 0) {
points.add(new Point(point)); //这里一定要new Point
}
//判断是否可以走0位置
if ((point.x = curPoint.x + 2) < X && (point.y = curPoint.y - 1) >= 0) {
points.add(new Point(point)); //这里一定要new Point
}
//判断是否可以走1位置
if ((point.x = curPoint.x + 2) < X && (point.y = curPoint.y + 1) < Y) {
points.add(new Point(point)); //这里一定要new Point
}
//判断是否可以走2位置
if ((point.x = curPoint.x + 1) < X && (point.y = curPoint.y + 2) < Y) {
points.add(new Point(point)); //这里一定要new Point
}
//判断是否可以走3位置
if ((point.x = curPoint.x - 1) >= 0 && (point.y = curPoint.y + 2) < Y) {
points.add(new Point(point)); //这里一定要new Point
}
//判断是否可以走4位置
if ((point.x = curPoint.x - 2) >= 0 && (point.y = curPoint.y + 1) < Y) {
points.add(new Point(point)); //这里一定要new Point
}
return points;
}
}贪心优化
1. 我们现在走的下一个位置,是按照顺时针来挑选位置,因此选择的这个点的下一个可走位置的个数不确定
2. 优化思路:应选择下一个的下一个可走位置较少的点开始走,以此减少回溯次数
3. 代码:对 ArrayList 集合按可走下一个位置的次数进行升序排序
java
public static void sort(ArrayList<Point> ps) {
ps.sort(new Comparator<Point>() {
@Override
public int compare(Point o1, Point o2) {
return next(o1).size() - next(o2).size();
}
});
}最终代码
java
import java.awt.*;
import java.util.ArrayList;
import java.util.Comparator;
public class HorseChessBoard {
// 初始化属性
// 棋盘大小
private static int X = 6;
private static int Y = 6;
// 棋盘
private static int[][] chessBoard = new int[Y][X];
// 是否访问过,用数组记录
private static boolean vistited[] = new boolean[X * Y];
// 记录是否遍历完棋盘
private static boolean finished = false;
// 主函数:测试
public static void main(String[] args) {
// 初始位置(坐标)
int row = 2;
int col = 2;
// 测试
long start = System.currentTimeMillis();
// 需要传入数组下标,因为是二维矩阵
traversalChessBoard(chessBoard, row - 1, col - 1, 1);
long end = System.currentTimeMillis();
System.out.println("执行耗时:" + (end - start));
// 打印结果
for (int[] rows : chessBoard) {
for (int val : rows) {
System.out.print(val + "\t");
}
System.out.println();
}
}
// 贪心优化,对可走点进行升序排序
public static void sort(ArrayList<Point> ps) {
ps.sort(new Comparator<Point>() {
@Override
public int compare(Point o1, Point o2) {
return next(o1).size() - next(o2).size();
}
});
}
// 核心代码,遍历棋盘
public static void traversalChessBoard(int[][] chessBoard, int row, int col, int step) {
// 把 step 记录到 chessBoard 中
chessBoard[row][col] = step;
// 设置该位置已经访问过(位置下标由二维矩阵推算)
vistited[row * X + col] = true;
// 获取从当前位置开始,下一个可以走的位置有哪些
ArrayList<Point> points = next(new Point(col, row)); // 主函数传入的起始坐标
// 贪心优化,先排序
sort(points);
// 遍历
while (!points.isEmpty()) {
// 取集合中的第一个点
Point p = points.remove(0);
// 判断是否走过
if (!vistited[p.y * X + p.x]) {
// 递归遍历(先传行再传列)
traversalChessBoard(chessBoard, p.y, p.x, step + 1);
}
}
// 遍历结束,判断是否走完棋盘,如果没有遍历成功就重置,然后回溯
if (step < X * Y && !finished) {
chessBoard[row][col] = 0;
vistited[row * X + col] = false;
} else {
finished = true;
}
}
// 创建ArrayList,用来存储可以走的位置(加入判断逻辑,该位置是否合理)
public static ArrayList<Point> next(Point curPoint) {
// 创建ArrayList
ArrayList<Point> points = new ArrayList<>();
// 创建 Point 对象
Point point = new Point();
//判断在 curPoint 是否可以走如下位置,如果可以走,就将该点(Point) 放入到points
//判断是否可以走5位置
if ((point.x = curPoint.x - 2) >= 0 && (point.y = curPoint.y - 1) >= 0) {
points.add(new Point(point)); //这里一定要new Point
}
//判断是否可以走6位置
if ((point.x = curPoint.x - 1) >= 0 && (point.y = curPoint.y - 2) >= 0) {
points.add(new Point(point)); //这里一定要new Point
}
//判断是否可以走7位置
if ((point.x = curPoint.x + 1) < X && (point.y = curPoint.y - 2) >= 0) {
points.add(new Point(point)); //这里一定要new Point
}
//判断是否可以走0位置
if ((point.x = curPoint.x + 2) < X && (point.y = curPoint.y - 1) >= 0) {
points.add(new Point(point)); //这里一定要new Point
}
//判断是否可以走1位置
if ((point.x = curPoint.x + 2) < X && (point.y = curPoint.y + 1) < Y) {
points.add(new Point(point)); //这里一定要new Point
}
//判断是否可以走2位置
if ((point.x = curPoint.x + 1) < X && (point.y = curPoint.y + 2) < Y) {
points.add(new Point(point)); //这里一定要new Point
}
//判断是否可以走3位置
if ((point.x = curPoint.x - 1) >= 0 && (point.y = curPoint.y + 2) < Y) {
points.add(new Point(point)); //这里一定要new Point
}
//判断是否可以走4位置
if ((point.x = curPoint.x - 2) >= 0 && (point.y = curPoint.y + 1) < Y) {
points.add(new Point(point)); //这里一定要new Point
}
return points;
}
}