Day 1

---

数组理论基础

文章链接：点击跳转

要求： 了解一下数组基础，以及数组的内存空间地址

704. 二分查找

题目建议：704.二分查找彻底掌握就可以，至于 35.搜索插入位置 和 34. 在排序数组中查找元素的第一个和最后一个位置 ，如果有时间就去看一下，没时间可以先不看，二刷的时候在看

今日要求：熟悉 根据 左闭右开，左闭右闭 两种区间规则 写出来的二分法

题目链接：https://leetcode.cn/problems/binary-search/

文章讲解：https://programmercarl.com/0704.二分查找.html

视频讲解：https://www.bilibili.com/video/BV1fA4y1o715

二分查找使用的前提条件

• 待查找的数据是有序的
• 数据不能有重复元素
• 数据必须存储在支持随机访问的结构中
• 数据范围需明确且固定

思路分析

这道题目的前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了

（1）左闭右闭 [a,b]

class Solution1 {
    public int search(int[] nums, int target) {
        // 避免当 target 小于nums[0] nums[nums.length - 1] 时多次循环运算
        if(target < nums[0] || target > nums[nums.length - 1]){
            return -1;
        }
        int left = 0;
        int right = nums.length - 1;
        // 因为 left = right 在区间上有意义，所以取等
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] > target) { // 更新右区间
                right = mid - 1; // 由区间的定义知 mid 可以被取到，下一轮比较不希望再比较 mid
            } else if (nums[mid] < target) {// 更新左区间
                left = mid + 1;
            } else { // 此时 num[mid] = target，返回下标
                return mid;
            }
        }
        return -1; // 没有找到
    }
}

代码分析

• 由区间的定义知，左右端点都可以取到
• 既然左右断点可以取到，即意味着 nums[mid] 这个值可以被取到，并且 left = right 是有意义的
• 在下一轮的搜索中是不希望再次搜索 nums[mid] 的，即更新区间为 mid 的左（右）端点
  • left = mid + 1
  • right = mid - 1

（2）左闭右开 [a,b)

class Solution2 {
    public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length; // 因为区间的定义是右区间的值取不到
        while (left < right){
            int mid = left + (right - left) / 2;
            if(nums[mid] > target){
                right = mid; // 在下一轮的搜索中就不会包含 nums[mid]
            }else if (nums[mid] < target){
                left = mid + 1;
            } else {
                return mid;
            }
        }
        return -1;
    }
}

代码分析

• 由区间的定义知，右端点是取不到的
• right 初始化为 nums.length，实际上取不到，即把 nums.length - 1 作为右断点
• 同理，我们还是希望在下一轮的搜索中不会再次搜索 nums[mid] 这个值
  • left = mid + 1：因为左区间是闭区间，左端点值可以取到，即下一次搜索不再搜索该端点
  • right = mid：因为有右区间是开区间，则下一次搜索会将 mid - 1 作为搜素区间的右端点

补充题目

• 35.搜索插入位置
• 34.在排序数组中查找元素的第一个和最后一个位置
• 69. x 的平方根
• 367. 有效的完全平方数

27. 移除元素

题目建议：建议先把暴力写法写一遍。 双指针法是本题的精髓，今日需要掌握，至于拓展题目可以先不看。

题目链接：https://leetcode.cn/problems/remove-element/

文章讲解：https://programmercarl.com/0027.移除元素.html

视频讲解：https://www.bilibili.com/video/BV12A4y1Z7LP

思路分析

由于数组的地址空间是连续的，只能通过元素值覆盖的方式删除元素

（1）暴力 for 循环

class Solution1 {
    // 暴力 for 循环
    public int removeElement(int[] nums, int val) {
        int size = nums.length;
        for (int i = 0; i < size; i++) {
            if (nums[i] == val) {
                for (int j = i + 1; j < size; j++) {
                    nums[j - 1] = nums[j];
                }
                i--; // 元素整体前移一位
                size--; // 删除一个 val，更新数组大小
            }
        }
        return size;
    }
}

代码分析

1. 使用 for 循环遍历，如果是 val，就执行删除操作（元素覆盖操作，删除位置后的所有元素前移一位）

2. 注意点

• 由于 val 位置后所有的元素前移了一位，此时指针 i 也要前移一位（原先指向的位置是 val，现在被后面的元素前移覆盖了）
• 每次删除一个元素之后，数组的大小需要减一

动图分析

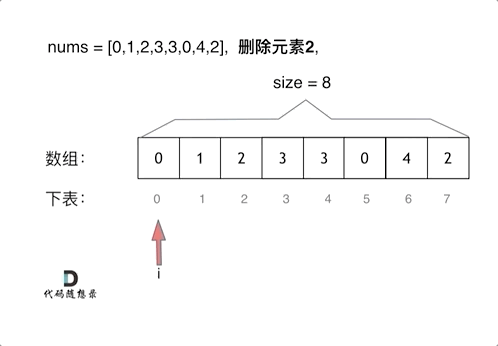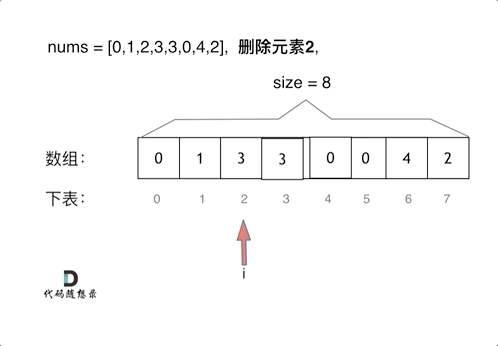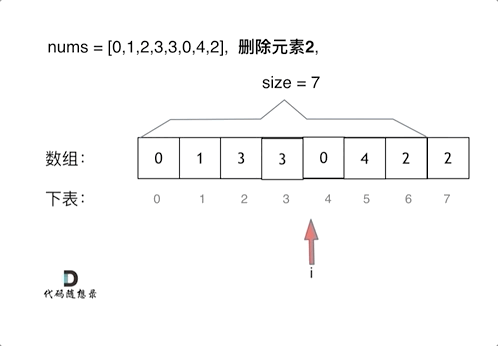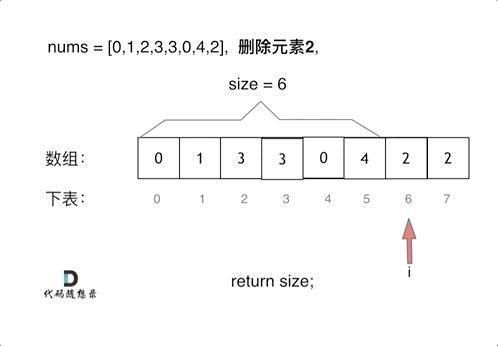
（2）双指针（快慢指针）

class Solution2 {
    // 双指针
    public int removeElement(int[] nums, int val) {
        int slow = 0;
        for (int fast = 0; fast < nums.length; fast++) {
            if(nums[fast] != val){
                nums[slow] = nums[fast];
                slow++;
            }
        }
        return slow;
    }
}

代码分析

1. 首先设置快慢指针

• slow：起始指向数组的第一个元素，用来更新新数组的元素
• fast：起始指向数组的第一个元素，用来寻找符合要求的元素

2. 删除过程的分析

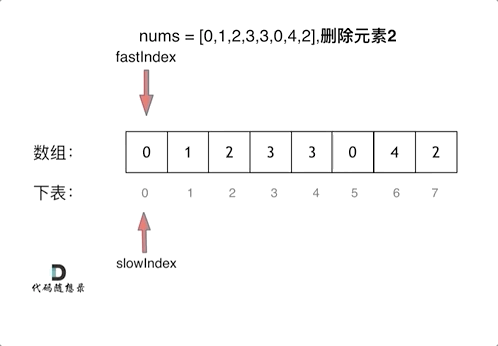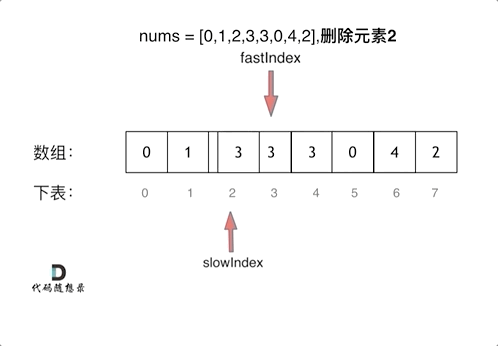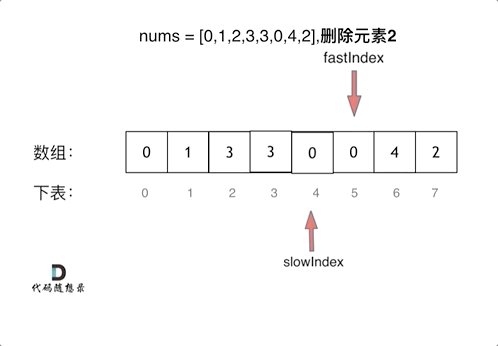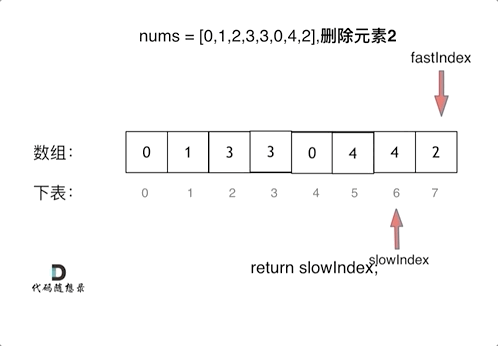
如果 fast 指向的元素不符合要求。此时 fast++,就会跳过这个元素，通过 slow 的移动，nums[slow] = nums[fast] 这个操作会覆盖不符合要求的元素同时原地更新新数组的元素，实现了删除操作

3. 更新过程分析

通过双指针移动，如果发现 fast 指向的值不是 val，则将 fast 指向的值赋给 slow 指向的位置，而 slow 指针正是用于更新新数组的元素

动图分析

补充题目

• 26.删除排序数组中的重复项
• 283.移动零
• 844.比较含退格的字符串
• 977. 有序数组的平方

977.有序数组的平方

题目建议： 本题关键在于理解双指针思想

题目链接：https://leetcode.cn/problems/squares-of-a-sorted-array/

文章讲解：https://programmercarl.com/0977.有序数组的平方.html

视频讲解： https://www.bilibili.com/video/BV1QB4y1D7ep

思路分析

• 数组平方后，大的值只可能在两边，可以使用相撞指针解决
• 题目要求返回新数组，可以让新数组的指针指向数组末尾，依次遍历、添加元素，最后得到的数组就是递增的
• 最暴力的方法：先平方，后排序，时间效率取决于排序算法的时间复杂度

（1）先平方，后排序

public class Solution1 {
    public int[] sortedSquares(int[] nums) {
        for (int i = 0; i < nums.length; i++) {
            nums[i] = nums[i] * nums[i];
        }
        for (int i = 0; i < nums.length - 1; i++) {
            for (int j = 0; j < nums.length - 1 - i; j++) {
                if(nums[j] > nums[j + 1]){
                    int temp = nums[j];
                    nums[j] = nums[j + 1];
                    nums[j + 1] = temp;
                }
            }
        }
        return nums;
    }
}

代码分析

• 首先采用 for 循环将数组的每个数做平方处理
• 然后采用冒泡排序对数组排序，得到有序平方后的数组

（2）双指针（相撞指针）

class Solution2{
    // 双指针思路
    public int[] sortedSquares(int[] nums) {
        int i = 0;
        int j = nums.length - 1;
        int[] result = new int[nums.length];
        int index = result.length - 1;
        while(i <= j){  // 取等是不为了遗漏二者相等时指向的元素
            if(nums[i] * nums[i] > nums[j] * nums[j]){
                result[index] =  nums[i] * nums[i];
                index--;
                i++;
            }else{ // 包含了相等的情况
                result[index] =  nums[j] * nums[j];
                index--;
                j--;
            }
        }
        return result;
    }
}

代码分析

• 首先使用 i、j 指针分别指向原始数组的第一个元素和最后一个元素
• i <= j（循环退出的条件）：确保党两个指针指向同一个元素时，这个元素可以被添加到新数组中，不会造成遗漏元素的情况
• 通过比较两个指针指向的值平方后的大小，把大的添加到新数组的末尾
  • 原数组指针前移（后移）
  • 新数组指着前移

总结

今日学习内容

• 二分思想
  • 使用前提
  • 使用场景
• 双指针
  • 快慢指针
  • 相撞指针