Day 32

---

后面的两道题目，都是完全背包的应用，做做感受一下

区别 01 背包

（1）完全背包中的物品数量是无限的

（2）物品、背包的遍历顺序可以颠倒

（3）原先对背包倒序遍历实现物品只放入一次，完全背包中使用正序遍历实现物品可以使用无数次

完全背包

题目链接：https://kamacoder.com/problempage.php?pid=1052

文章讲解：https://programmercarl.com/背包问题理论基础完全背包.html

视频讲解：https://www.bilibili.com/video/BV1uK411o7c9

思路分析

（1）确定 dp 数组以及下标的含义

dp [ i ] [ j ] 表示从下标为 [ 0 - i ] 的物品，每个物品可以取无限次，放进容量为 j 的背包，价值总和最大是多少

（2） 确定递推公式

在完全背包中，物品是可以放无限个，所以即使空出物品 1 空间重量，那背包中也可能还有物品 1，所以此时我们依然考虑放物品 0 和物品 1 的最大价值即：dp [ 1 ] [ 1] ，而不是 dp [ 0 ] [ 1 ]

所以 放物品 1 的情况 = dp [ 1 ] [ 1 ] + 物品 1 的价值

dp [ i ] [ j ] = max ( dp [ i - 1 ] [ j ] , dp [ i ] [ j - weight [ i ] ] + value [ i ] )

（3） dp 数组如何初始化

物品	重量	价值
物品 0	1	15
物品 1	3	20
物品 2	4	30

dp [ 0 ] [ j ] 如果能放下 weight [ 0 ]的话，就一直装，每一种物品有无限个

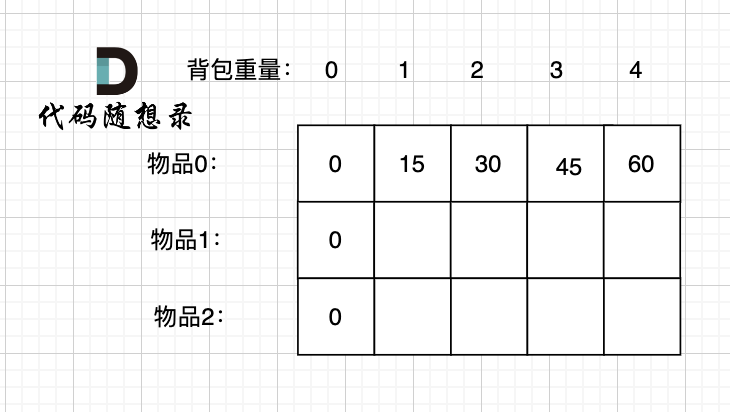
（4） 确定遍历顺序

采用正序遍历实现物品可以使用无数次

先遍历物品，后遍历背包，反过来也可以

（5）举例推导 dp 数组

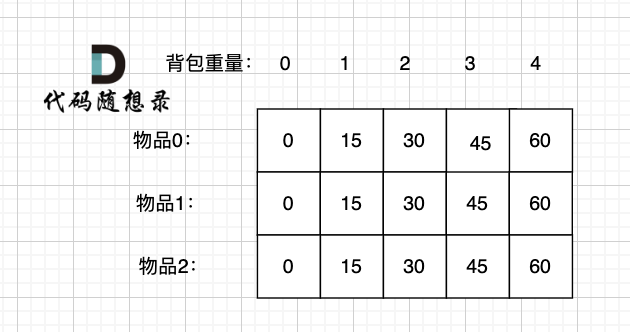
二维 dp

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int bagWeight = scanner.nextInt();

        int[] weight = new int[n];
        int[] value = new int[n];

        for (int i = 0; i < n; i++) {
            weight[i] = scanner.nextInt();
            value[i] = scanner.nextInt();
        }

        int[][] dp = new int[n][bagWeight + 1];

        // 初始化

        // 背包容量为 0，无法放下任何物品，价值为0
        for (int i = 0; i < n; i++) {
            dp[i][0] = 0;
        }

        // 完全背包，同一物品可以使用多次
        for (int j = weight[0]; j <= bagWeight; j++) {
            dp[0][j] = dp[0][j - weight[0]] + value[0];
        }

        // dp

        // 先遍历物品
        for (int i = 1; i < n; i++) {
            // 后遍历背包，采用正序遍历
            for (int j = 0; j <= bagWeight; j++) {
                // 当前背包的容量 j 小于当前物品需要的容量（不放物品 i）
                if (j < weight[i]) {
                    dp[i][j] = dp[i - 1][j];
                } else {
                    // 放物品 i
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);
                }
            }
        }
        System.out.println(dp[n - 1][bagWeight]);
    }
}

518. 零钱兑换 II

题目链接：https://leetcode.cn/problems/coin-change-ii/

文章讲解：https://programmercarl.com/0518.零钱兑换II.html

视频讲解：https://www.bilibili.com/video/BV1KM411k75j

思路分析

一维 dp 中的遍历顺序

（1）求组合数：先遍历物品，后遍历背包

（2）求排列数：先遍历背包，后遍历物品

一维 dp

class Solution {
    public int change(int amount, int[] coins) {
        int[] dp = new int[amount + 1];
        // 什么也不装，这是一种情况
        dp[0] = 1;
        // 求组合数，先遍历物品，后遍历背包
        for (int i = 0; i < coins.length; i++) {
            for (int j = coins[i]; j <= amount; j++) {
                dp[j] += dp[j - coins[i]];
            }
        }
        return dp[amount];
    }
}

二维 dp

class Solution {
    public int change(int amount, int[] coins) {
        int[][] dp = new int[coins.length][amount + 1];

        // 初始化左边列
        for (int i = 0; i < coins.length; i++) {
            dp[i][0] = 1;
        }

        // 初始化上边行
        for (int i = coins[0]; i <= amount; i++) {
            dp[0][i] += dp[0][i - coins[0]];
        }

        for (int i = 1; i < coins.length; i++) {
            for (int j = 1; j <= amount; j++) {
                // 不放物品 i（背包容量不够）
                if (j < coins[i]){
                    dp[i][j] = dp[i - 1][j];
                }else {
                    // 放物品 i
                    dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]];
                }
            }
        }
        return dp[coins.length - 1][amount];
    }
}

377. 组合总和 Ⅳ

题目链接：https://leetcode.cn/problems/combination-sum-iv/

文章讲解：https://programmercarl.com/0377.组合总和Ⅳ.html

视频讲解：https://www.bilibili.com/video/BV1V14y1n7B6

思路分析

本题是完全背包中求排列的应用场景，代码和上题大同小异

一维 dp

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target + 1];
        dp[0] = 1;
        // 求组合数，先遍历背包，后遍历物品
        for (int i = 0; i <= target; i++) {
            for (int j = 0; j < nums.length; j++) {
                if (i >= nums[j]) {
                    dp[i] += dp[i - nums[j]];
                }
            }
        }
        return dp[target];
    }
}

70. 爬楼梯 （进阶）

这道题目 爬楼梯之前我们做过，这次再用完全背包的思路来分析一遍

题目链接：https://kamacoder.com/problempage.php?pid=1067

文章讲解：https://programmercarl.com/0070.爬楼梯完全背包版本.html

思路分析

看文章讲解；如何将次场景迁移到完全背包求排列数问题

一维 dp

import java.util.Scanner;

public class climbStairs {
    public static void main(String[] args) {
        // 爬的每一阶台阶对应物品，楼顶对应背包

        Scanner scanner = new Scanner(System.in);
        int m, n;
        while (scanner.hasNextInt()) {
            n = scanner.nextInt();
            m = scanner.nextInt();

            int[] dp = new int[n + 1];
            dp[0] = 1;
            // 排列问题，先遍历背包后遍历物品
            for (int j = 1; j <= n; j++) {
                for (int i = 1; i <= m; i++) {
                    if (j - i >= 0) {
                        dp[j] += dp[j - i];
                    }
                }
            }
        System.out.println(dp[n]);
        }
    }
}