Day 18

---

669. 修剪二叉搜索树

这道题目比较难，比添加增加和删除节点难的多，建议先看视频理解。

题目链接：https://leetcode.cn/problems/trim-a-binary-search-tree/

文章讲解：https://programmercarl.com/0669.修剪二叉搜索树.html

视频讲解： https://www.bilibili.com/video/BV17P41177ud

思路分析

在有了删除节点二叉树的基础上，删除的核心就是把应当重接的节点返回给上一层，通过函数递归实现二叉搜索树的修剪，这里只需要考虑不在范围内的两种情况如何处理即可

题解

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null) {
            return null;
        }
        // 根据二叉搜索树的特性，如果比最小值还小，应当返回比root.val大一点的值，即返回右子树
        if (root.val < low) {
            TreeNode right = trimBST(root.right, low, high);
            return right;
        }
        // 根据二叉搜索树的特性，如果比最大值还大，应当返回比root.val小一点的值，即返回左子树
        if (root.val > high) {
            TreeNode left = trimBST(root.left, low, high);
            return left;
        }
        // root在[low,high]范围内
        root.left = trimBST(root.left, low, high); // 递归修剪左子树
        root.right = trimBST(root.right, low, high); // 递归修剪右子树
        return root;
    }
}

108.将有序数组转换为二叉搜索树

本题就简单一些，可以尝试先自己做做。

题目链接：https://leetcode.cn/problems/convert-sorted-array-to-binary-search-tree

文章讲解：https://programmercarl.com/0108.将有序数组转换为二叉搜索树.html

视频讲解：https://www.bilibili.com/video/BV1uR4y1X7qL

思路分析

二叉树与数组相结合，本质就是寻找分割点，分割点作为当前节点，然后递归左区间和右区间，本题要求是平衡二叉树，不应该被平衡的定义所困扰，从数组的中间节点分割，递归处理左右子树，这样就可以实现节点个数分布均匀，其次数组还是有序的，这正好满足二叉搜索树的特性

题解

class Solution {
	public TreeNode sortedArrayToBST(int[] nums) {
		TreeNode root = traversal(nums, 0, nums.length - 1);
		return root;
	}

	// 左闭右闭区间[left, right]
	private TreeNode traversal(int[] nums, int left, int right) {
		if (left > right) return null;

		int mid = left + ((right - left) >> 1); // 找到中间节点
		TreeNode root = new TreeNode(nums[mid]); // 中间节点作为根节点
		root.left = traversal(nums, left, mid - 1); // 递归创建左子树
		root.right = traversal(nums, mid + 1, right); // 递归创建右子树
		return root;
	}
}

538.把二叉搜索树转换为累加树

本题也不难，在 求二叉搜索树的最小绝对差 和 众数 那两道题目 都讲过了 双指针法，思路是一样的。

题目链接：https://leetcode.cn/problems/convert-bst-to-greater-tree

文章讲解：https://programmercarl.com/0538.把二叉搜索树转换为累加树.html

视频讲解：https://www.bilibili.com/video/BV1d44y1f7wP

思路分析

首先是二叉搜索树，需要把握其特性

题目中是找比本身节点大的，很容易可以想到从右子树开始遍历

于是确定遍历顺序：右中左，使用双指针法实现数值累加

题解

public class Solution {
    int pre;  // 定义前驱指针记录节点的数值

    public TreeNode convertBST(TreeNode root) {
        convertBST1(root);
        return root;
    }

    // 按右中左顺序遍历，累加即可
    public void convertBST1(TreeNode root) {
        if (root == null) {
            return;
        }
        convertBST1(root.right);
        root.val += pre;
        pre = root.val;
        convertBST1(root.left);
    }
}

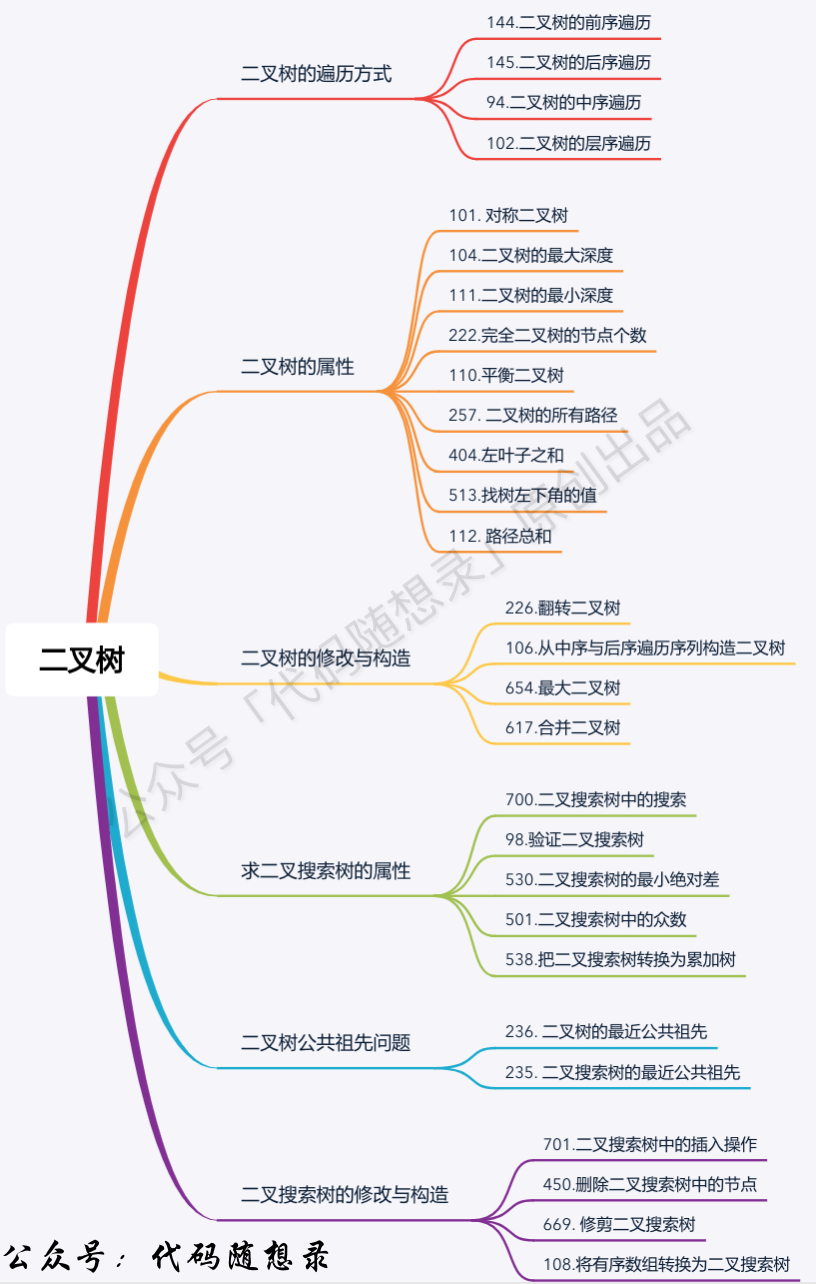
阶段六结束：二叉树总结

文章链接：https://programmercarl.com/二叉树总结篇.html