Day 40

---

647. 回文子串

动态规划解决的经典题目，如果没接触过的话，别硬想 直接看题解。

题目链接：https://leetcode.cn/problems/palindromic-substrings

文章讲解：https://programmercarl.com/0647.回文子串.html

视频讲解：https://www.bilibili.com/video/BV17G4y1y7z9

思路分析

dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是 dp[i][j]为 true，否则为 false

当 s[i]与 s[j]不相等，那没啥好说的了，dp[i][j]一定是 false

当 s[i]与 s[j]相等时，这就复杂一些了，有如下三种情况

情况一：下标 i 与 j 相同，同一个字符例如 a，当然是回文子串

情况二：下标 i 与 j 相差为 1，例如 aa，也是回文子串

情况三：下标：i 与 j 相差大于 1 的时候，例如 cabac，此时 s[i]与 s[j]已经相同了，我们看 i 到 j 区间是不是回文子串就看 aba 是不是回文就可以了，那么 aba 的区间就是 i+1 与 j-1 区间，这个区间是不是回文就看 dp[i + 1][j - 1]是否为 true

二维 dp

class Solution {
    public int countSubstrings(String s) {
        char[] chars = s.toCharArray();
        int len = chars.length;
        boolean[][] dp = new boolean[len][len];
        int result = 0;

        for (int i = len - 1; i >= 0; i--) {
            for (int j = i; j < len; j++) {
                if (chars[i] == chars[j]) {
                    if (j - i <= 1) {
                        result++;
                        dp[i][j] = true;
                    } else if (dp[i + 1][j - 1]) {
                        result++;
                        dp[i][j] = true;
                    }
                }
            }
        }
        return result;
    }
}

516.最长回文子序列

647. 回文子串，求的是回文子串，而本题要求的是回文子序列， 大家要搞清楚两者之间的区别。

题目链接：https://leetcode.cn/problems/longest-palindromic-subsequence

文章讲解：https://programmercarl.com/0516.最长回文子序列.html

视频讲解：https://www.bilibili.com/video/BV1d8411K7W6

思路分析

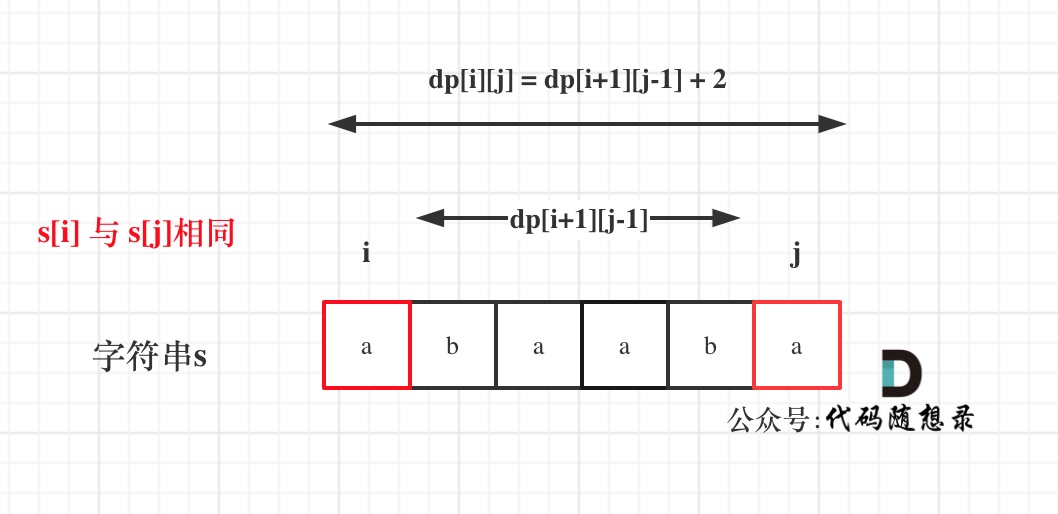
dp[i][j]：字符串 s 在[i, j]范围内最长的回文子序列的长度为 dp[i][j]

如果 s[i]与 s[j]相同，那么 dp[i][j] = dp[i + 1][j - 1] + 2

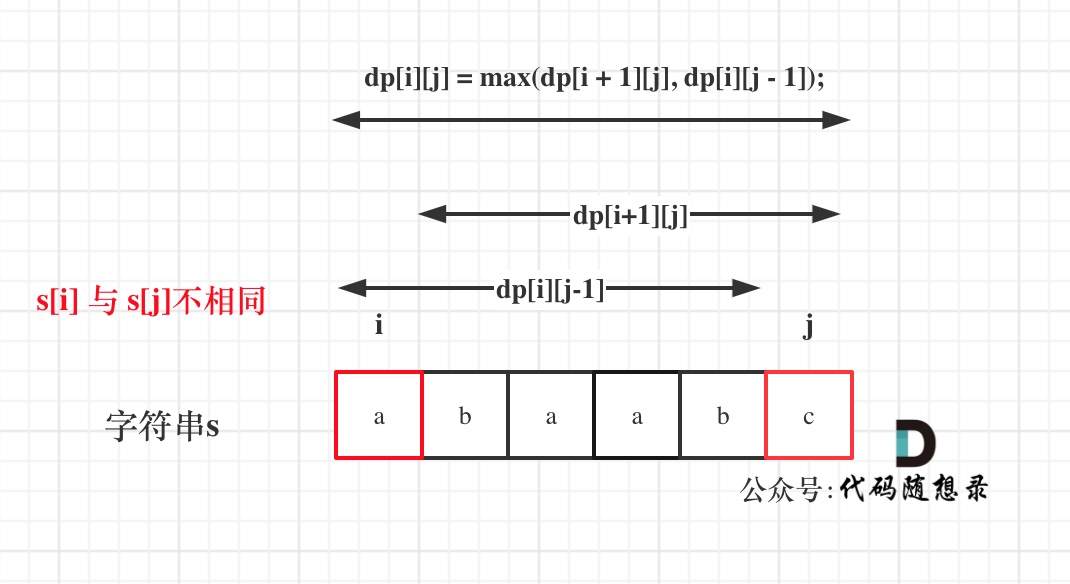
如果 s[i]与 s[j]不相同，说明 s[i]和 s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度，那么分别加入 s[i]、s[j]看看哪一个可以组成最长的回文子序列

加入 s[j]的回文子序列长度为 dp[i + 1][j]，加入 s[i]的回文子序列长度为 dp[i][j - 1]

那么 dp[i][j]一定是取最大的，即：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])

二维 dp

class Solution {
    public int longestPalindromeSubseq(String s) {
        int len = s.length();
        int[][] dp = new int[len][len];
        for (int i = len - 1; i >= 0; i--) {
            dp[i][i] = 1; // 单个字符的最长子序列长度为本身
            for (int j = i + 1; j < len; j++) {
                if (s.charAt(i) == s.charAt(j)) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
                    dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[0][len - 1];
    }
}

动态规划总结篇

文章讲解：https://programmercarl.com/动态规划总结篇.html