Day 47

---

并查集理论基础

并查集理论基础很重要，明确并查集解决什么问题，代码如何写，对后面做并查集类题目很有帮助。

文章讲解：https://www.programmercarl.com/kamacoder/图论并查集理论基础.html

视频讲解：https://www.bilibili.com/video/BV1pFjUzvES2

应用场景

（1）并查集常用来解决连通性问题，大白话就是当我们需要判断两个元素是否在同一个集合里的时候，我们就要想到用并查集

（2）并查集主要有两个功能

将两个元素添加到一个集合中

判断两个元素在不在同一个集合

判断是否成环（加入每一组边，如果发现新加入边已经在集合里，则表明成环）

我们将三个元素 A，B，C （分别是数字）放在同一个集合，其实就是将三个元素连通在一起，如何连通呢？

只需要用一个一维数组来表示，即：father[A] = B，father[B] = C 这样就表述 A 与 B 与 C 连通了（有向连通图）

模板代码

class DisJoint {
    private int[] father;

    public DisJoint(int N) {
        father = new int[N];
        // 初始时根节点为本身
        for (int i = 0; i < N; i++) {
            father[i] = i;
        }
    }

    // 寻找根节点
    public int find(int n) {
        // 找到根节点就返回
        if (n == father[n]) {
            return n;
        }
        // 递归查找
        return find(father[n]);
    }

    // 通过根节点链接关系确定两个元素在同一个集合中
    public void join(int n, int m) {
        // 首先判断是否在同一个集合中，不要重复添加
        n = find(n);
        m = find(m);
        if (n == m) {
            return;
        }
        father[m] = n;
    }

    // 如果根节点相同，则说明在一个集合中
    public boolean isSame(int n, int m) {
        n = find(n);
        m = find(m);
        return m == n;
    }
}

路径压缩优化

（1）递归搜索过程，如果这棵多叉树高度很深的话，每次 find 函数 去寻找根的过程就要递归很多次

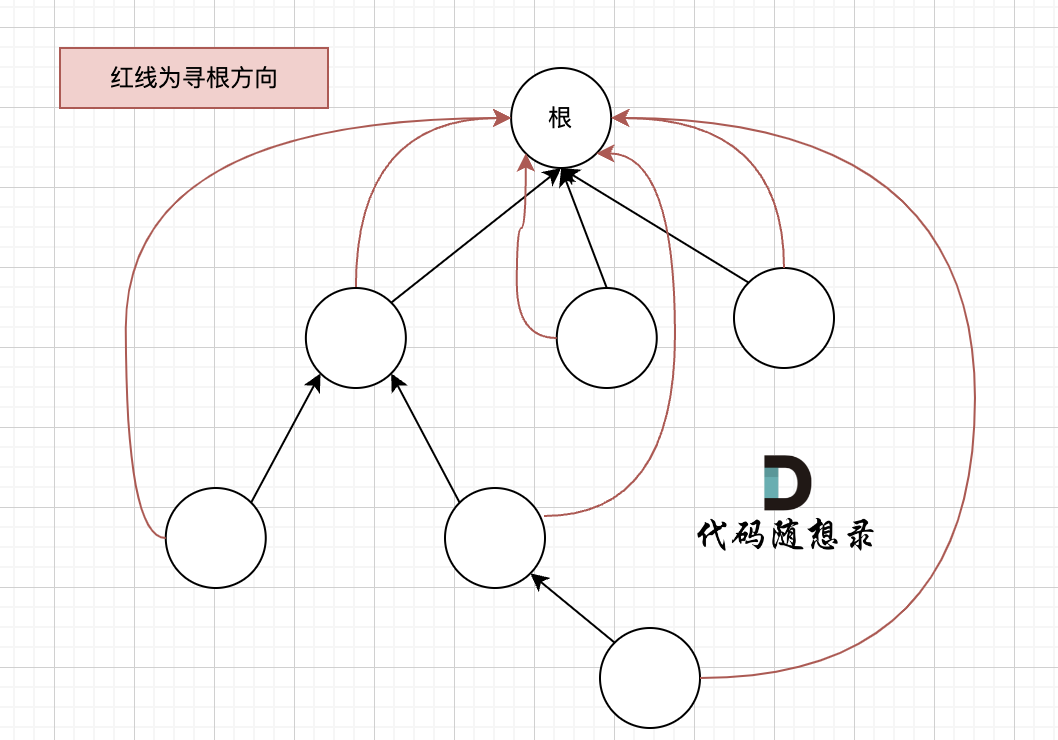
（2）路径压缩，我们的目的只需要知道这些节点在同一个根下就可以，所以对这棵多叉树的构造只需要这样就可以了

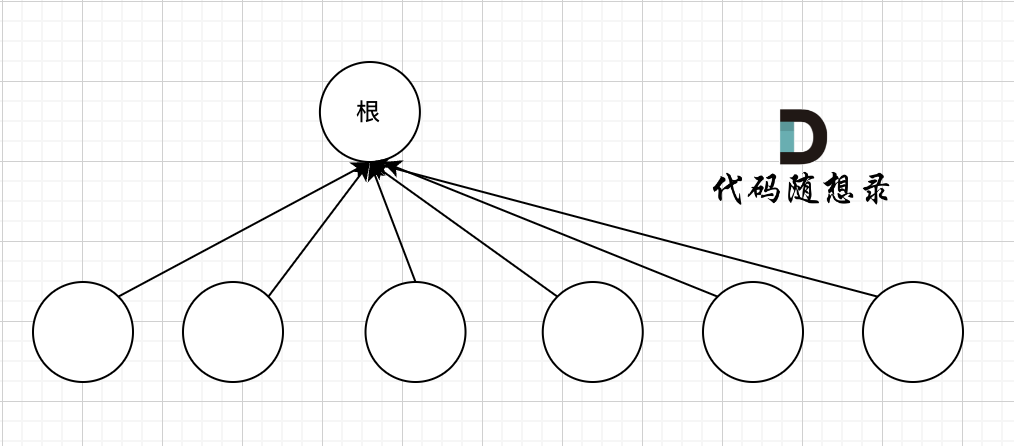
find 函数向上寻找根节点，father[u] 表述 u 的父节点，那么让 father[u] 直接获取 find 函数返回的根节点，这样就让节点 u 的父节点变成根节点

...

// 寻找根节点
public int find(int n) {
    // 找到根节点就返回
    if (n == father[n]) {
        return n;
    }
    // 递归查找
    // return find(father[n]);

    // find(father[n]) 返回的是 n 的根节点，
    // 直接赋值给 father[n]（n 的父节点），
    // 让 n 的父节点变成根节点，实现了路径压缩
    return father[n] = find(father[n]);
}

...

寻找存在的路径

并查集裸题，学会理论基础后，本题直接可以直接刷过

题目链接：https://kamacoder.com/problempage.php?pid=1179

文章讲解：https://www.programmercarl.com/kamacoder/0107.寻找存在的路径.html

视频讲解：https://www.bilibili.com/video/BV1k3T7zWEVj

思路分析

变相理解题意，一个节点能否到达下一个节点其实就是问两个节点是否在同一个集合中

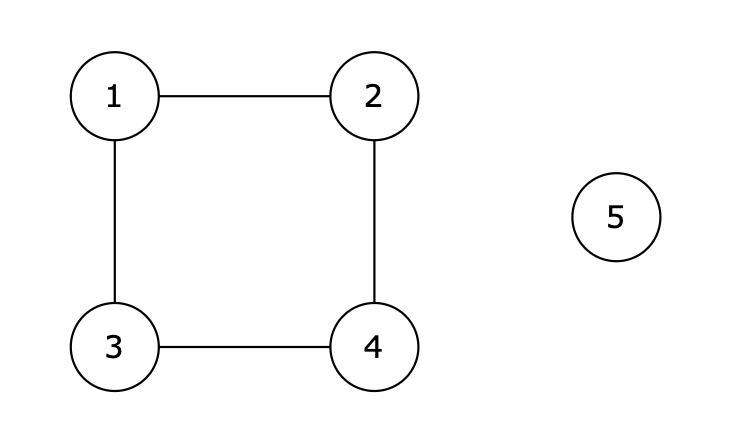
题意示例如上图，示例中的 source = 1，destination = 4，即判断 1 和 4 是否在同一个集合中

题解

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        int N, M;
        Scanner scanner = new Scanner(System.in);
        // N 个节点，M 条边
        N = scanner.nextInt();
        M = scanner.nextInt();

        DisJoint disJoint = new DisJoint(N);

        // 录入边
        for (int i = 0; i < M; i++) {
            disJoint.join(scanner.nextInt(), scanner.nextInt());
        }

        // 录入 source 和 destination，并判断是否在同一个集合中
        if (disJoint.isSame(scanner.nextInt(), scanner.nextInt())){
            System.out.println("1");
        }else {
            System.out.println("0");
        }
    }
}

class DisJoint {
    private int[] father;

    public DisJoint(int N) {
        // 节点编号是从 1 到 N
        father = new int[N + 1];

        // 初始时指向自己
        for (int i = 1; i <= N; i++) {
            father[i] = i;
        }
    }

    // 寻找根节点
    public int find(int n) {
        // 找到根节点就返回
        if (n == father[n]) {
            return n;
        }
        // 递归查找
        return find(father[n]);
    }

    // 通过根节点链接关系确定两个元素在同一个集合中
    public void join(int n, int m) {
        // 首先判断是否在同一个集合中，不要重复添加
        n = find(n);
        m = find(m);
        if (n == m) {
            return;
        }
        father[m] = n;
    }

    // 如果根节点相同，则说明在一个集合中
    public boolean isSame(int n, int m) {
        n = find(n);
        m = find(m);
        return m == n;
    }
}