Day 14
14. 找树左下角的值
本题递归偏难,反而迭代简单属于模板题, 两种方法掌握一下
题目链接:https://leetcode.cn/problems/find-bottom-left-tree-value
文章讲解:https://programmercarl.com/0513.找树左下角的值.html
视频讲解:https://www.bilibili.com/video/BV1424y1Z7pn
思路分析
易错点:需要注意审题,两个条件,最底层、最左边,意味着不只是左孩子,右孩子也可能符合条件
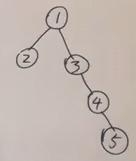
遍历顺序:前中后三者都可,此题对遍历顺序中的根节点无需处理,只要确保遍历顺序是优先遍历左子树,然后遍历右子树即可
递归法
class Solution {
private int Deep = -1;
private int value = 0;
public int findBottomLeftValue(TreeNode root) {
value = root.val;
findLeftValue(root, 0);
return value;
}
private void findLeftValue(TreeNode root, int deep) {
if (root == null) {
return;
}
// 判断叶子节点
if (root.left == null && root.right == null) {
if (deep > Deep) {
value = root.val;
Deep = deep;
}
}
// 递归遍历左子树
if (root.left != null) {
deep++;
findLeftValue(root.left, deep);
deep--; // 体现回溯的过程
}
// 递归遍历右子树
if (root.right != null) {
deep++;
findLeftValue(root.right, deep);
deep--; // 体现回溯的过程
}
}
}层序遍历
每一层的第一个节点一定是最左节点,当循环结束时正好是遍历到最后一层,使用层序遍历逻辑相对容易理解
class Solution {
public int findBottomLeftValue(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int res = 0;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode poll = queue.poll();
if (i == 0) {
res = poll.val;
}
if (poll.left != null) {
queue.offer(poll.left);
}
if (poll.right != null) {
queue.offer(poll.right);
}
}
}
return res;
}
}112. 路径总和
本题 又一次涉及到回溯的过程,而且回溯的过程隐藏的还挺深,建议先看视频来理解
题目连接:https://leetcode.cn/problems/path-sum
文章讲解:https://programmercarl.com/0112.路径总和.html
视频讲解:https://www.bilibili.com/video/BV19t4y1L7CR
思路分析
本题无需处理中间节点,前中后三种遍历顺序都可以,只要找到一条路径就结束,这里需要把每一个节点的处理结果返回给上一层节点,判断当前遍历的路径是否是符合条件的路径
题解
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null) {
return false;
}
targetSum -= root.val;
// 叶子结点
if (root.left == null && root.right == null) {
return targetSum == 0;
}
if (root.left != null) {
boolean left = hasPathSum(root.left, targetSum);
if (left) { // 已经找到,提前返回
return true;
}
}
if (root.right != null) {
boolean right = hasPathSum(root.right, targetSum);
if (right) { // 已经找到,提前返回
return true;
}
}
return false;
}
}113. 路径总和 ii
题目链接:https://leetcode.cn/problems/path-sum-ii
思路分析
本题是上一题的扩展,区别在于本题需要记录符合条件的路径
题解
class Solution {
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) return res; // 非空判断
List<Integer> path = new LinkedList<>();
preOrderDfs(root, targetSum, res, path);
return res;
}
public void preOrderDfs(TreeNode root, int targetSum, List<List<Integer>> res, List<Integer> path) {
path.add(root.val);
// 遇到了叶子节点
if (root.left == null && root.right == null) {
// 找到了和为 targetsum 的路径
if (targetSum - root.val == 0) {
res.add(new ArrayList<>(path));
}
return; // 如果和不为 targetsum,返回
}
if (root.left != null) {
preOrderDfs(root.left, targetSum - root.val, res, path);
path.remove(path.size() - 1); // 回溯
}
if (root.right != null) {
preOrderDfs(root.right, targetSum - root.val, res, path);
path.remove(path.size() - 1); // 回溯
}
}
}106.从中序与后序遍历序列构造二叉树
从中序与后序遍历序列构造二叉树
本题算是比较难的二叉树题目了,大家先看视频来理解
题目链接:https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal
文章讲解:https://programmercarl.com/0106.从中序与后序遍历序列构造二叉树.html
视频讲解:https://www.bilibili.com/video/BV1vW4y1i7dn
思路分析
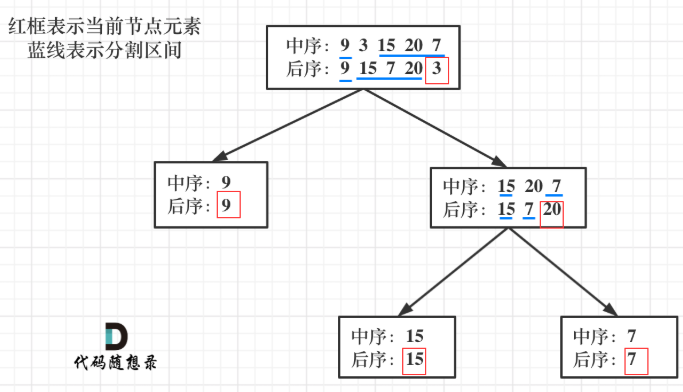
第一步:如果数组大小为零的话,说明是空节点了
第二步:如果不为空,那么取后序数组最后一个元素作为节点元素
第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
第五步:切割后序数组,切成后序左数组和后序右数组
第六步:递归处理左区间和右区间
常规思路
class Solution {
/*
postorder:后序遍历
inorder:中序遍历
*/
public TreeNode buildTree(int[] inorder, int[] postorder) {
if (postorder.length == 0 || inorder.length == 0)
return null;
return buildHelper(inorder, 0, inorder.length, postorder, 0, postorder.length);
}
private TreeNode buildHelper(int[] inorder, int inorderStart, int inorderEnd, int[] postorder, int postorderStart, int postorderEnd) {
if (postorderStart == postorderEnd)
return null;
// 后序遍历:左右根,最后一定是根节点
int rootVal = postorder[postorderEnd - 1];
// 构造节点
TreeNode root = new TreeNode(rootVal);
// 后序数组中找到了根节点,在中序数组中找到根节点的位置,进行切割
int middleIndex;
for (middleIndex = inorderStart; middleIndex < inorderEnd; middleIndex++) {
if (inorder[middleIndex] == rootVal)
break;
}
// 中序数组中根节点的左子树索引范围
int leftInorderStart = inorderStart;
int leftInorderEnd = middleIndex;
// 中序数组中根节点的右子树索引范围
int rightInorderStart = middleIndex + 1;
int rightInorderEnd = inorderEnd;
// 依据后序数组中根节点在中序数组中分割出左右子树
// 在后序数组中分割出左子树
/*
后序遍历顺序:左右根
后序数组的左子树
起始位置:后序数组的起始位置
终止位置:根据中序数组中根节点的位置来计算左子树的的节点个数,得到终止位置的索引
*/
int leftPostorderStart = postorderStart;
int leftPostorderEnd = postorderStart + (middleIndex - inorderStart);
// 在后序数组中分割出右子树
/*
后序数组中计算出左子树的基础上,除了最后一个位置是根节点,剩余部分就是右子树的索引部分
*/
int rightPostorderStart = leftPostorderEnd;
int rightPostorderEnd = postorderEnd - 1;
// 递归创建左右子树
root.left = buildHelper(inorder, leftInorderStart, leftInorderEnd, postorder, leftPostorderStart, leftPostorderEnd);
root.right = buildHelper(inorder, rightInorderStart, rightInorderEnd, postorder, rightPostorderStart, rightPostorderEnd);
// 返回根节点
return root;
}
}map 优化
class Solution {
Map<Integer, Integer> map; // 方便根据数值查找位置
public TreeNode buildTree(int[] inorder, int[] postorder) {
map = new HashMap<>();
for (int i = 0; i < inorder.length; i++) { // 用map保存中序序列的数值对应位置
map.put(inorder[i], i);
}
return findNode(inorder, 0, inorder.length, postorder,0, postorder.length); // 前闭后开
}
public TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd) {
// 参数里的范围都是前闭后开
if (inBegin >= inEnd || postBegin >= postEnd) { // 不满足左闭右开,说明没有元素,返回空树
return null;
}
int rootIndex = map.get(postorder[postEnd - 1]); // 找到后序遍历的最后一个元素在中序遍历中的位置
TreeNode root = new TreeNode(inorder[rootIndex]); // 构造结点
int lenOfLeft = rootIndex - inBegin; // 保存中序左子树个数,用来确定后序数列的个数
root.left = findNode(inorder, inBegin, rootIndex,
postorder, postBegin, postBegin + lenOfLeft);
root.right = findNode(inorder, rootIndex + 1, inEnd,
postorder, postBegin + lenOfLeft, postEnd - 1);
return root;
}
}105.从前序与中序遍历序列构造二叉树
题目链接:https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal
思路分析
本质是一样的,只不过是从后序变成了前序
常规思路
class Solution {
/*
preorder:前序遍历
inorder:中序遍历
*/
public TreeNode buildTree(int[] preorder, int[] inorder) {
if (preorder.length == 0 || inorder.length == 0)
return null;
return buildHelper(inorder, 0, inorder.length, preorder, 0, preorder.length);
}
private TreeNode buildHelper(int[] inorder, int inorderStart, int inorderEnd, int[] preorder, int preorderStart, int preorderEnd) {
if (preorderStart == preorderEnd || inorderStart == inorderEnd)
return null;
// 前序遍历:根左右,第一个元素一定是根节点
int rootVal = preorder[preorderStart];
// 构造节点
TreeNode root = new TreeNode(rootVal);
// 在中序数组中找到根节点的位置,来划分左右子树
int middleIndex = inorderStart;
while (inorder[middleIndex] != rootVal) {
middleIndex++;
}
// 中序数组中根节点的左子树索引范围
int leftInorderStart = inorderStart;
int leftInorderEnd = middleIndex;
// 中序数组中根节点的右子树索引范围
int rightInorderStart = middleIndex + 1;
int rightInorderEnd = inorderEnd;
// 前序数组中,根节点之后是左子树,左子树的节点数为 middleIndex - inorderStart
int leftPreorderStart = preorderStart + 1;
int leftPreorderEnd = leftPreorderStart + (middleIndex - inorderStart);
// 右子树从左子树结束后的位置开始
int rightPreorderStart = leftPreorderEnd;
int rightPreorderEnd = preorderEnd;
// 递归构建左右子树
root.left = buildHelper(inorder, leftInorderStart, leftInorderEnd, preorder, leftPreorderStart, leftPreorderEnd);
root.right = buildHelper(inorder, rightInorderStart, rightInorderEnd, preorder, rightPreorderStart, rightPreorderEnd);
// 返回根节点
return root;
}
}map 优化
class Solution {
Map<Integer, Integer> map;
public TreeNode buildTree(int[] preorder, int[] inorder) {
map = new HashMap<>();
for (int i = 0; i < inorder.length; i++) { // 用map保存中序序列的数值对应位置
map.put(inorder[i], i);
}
return findNode(preorder, 0, preorder.length, inorder, 0, inorder.length); // 前闭后开
}
public TreeNode findNode(int[] preorder, int preBegin, int preEnd, int[] inorder, int inBegin, int inEnd) {
// 参数里的范围都是前闭后开
if (preBegin >= preEnd || inBegin >= inEnd) { // 不满足左闭右开,说明没有元素,返回空树
return null;
}
int rootIndex = map.get(preorder[preBegin]); // 找到前序遍历的第一个元素在中序遍历中的位置
TreeNode root = new TreeNode(inorder[rootIndex]); // 构造结点
int lenOfLeft = rootIndex - inBegin; // 保存中序左子树个数,用来确定前序数列的个数
root.left = findNode(preorder, preBegin + 1, preBegin + lenOfLeft + 1,
inorder, inBegin, rootIndex);
root.right = findNode(preorder, preBegin + lenOfLeft + 1, preEnd,
inorder, rootIndex + 1, inEnd);
return root;
}
}