Day 20
39. 组合总和
本题是 集合里元素可以用无数次,那么和组合问题的差别 其实仅在于 startIndex 上的控制
题目链接:https://leetcode.cn/problems/combination-sum
文章讲解:https://programmercarl.com/0039.组合总和.html
视频讲解:https://www.bilibili.com/video/BV1KT4y1M7HJ
思路分析
本题不一样的点在于没有限定组合元素的个数,并且元素可以重复使用,只需要找到和为 target 的组合就可
剪枝分析
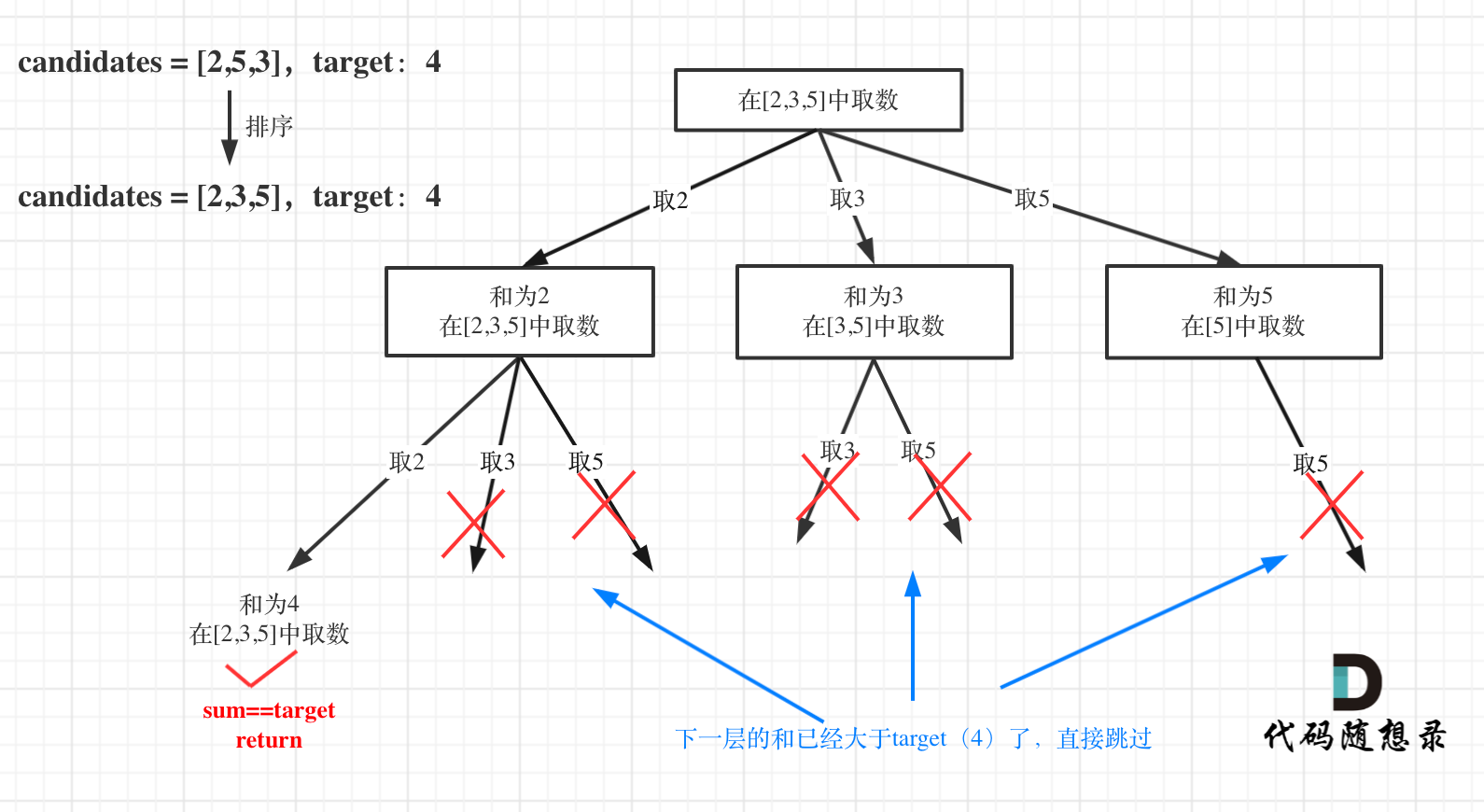
(1)对于 sum 已经大于 target 的情况,其实是依然进入了下一层递归,只是下一层递归结束判断的时候,会判断 sum > target 的话就返回
(2)其实如果已经知道下一层的 sum 会大于 target,就没有必要进入下一层递归了。
(3)剪枝:对总集合排序之后,如果下一层的 sum(就是本层的 sum + candidates[i])已经大于 target,就可以结束本轮 for 循环的遍历
题解(剪枝)
java
class Solution {
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
// 对数组排序,依次从小到大累加,将 sum 与 target 比较,方便剪枝
Arrays.sort(candidates);
backtracking(candidates,target,0,0);
return res;
}
public void backtracking(int[] candidates, int target, int sum, int startindex) {
if (sum > target){
return;
}
if (sum == target) {
res.add(new ArrayList<>(path));
return;
}
for (int i = startindex; i < candidates.length; i++) {
// 剪枝,如果 sum + candidates[i] > target,就没有必要进行下一层递归,直接结束
if (sum + candidates[i] > target) {
break;
}
path.add(candidates[i]);
sum += candidates[i];
// 因为元素可以重复使用,所以传 i(下一层递归的起点)
backtracking(candidates, target, sum , i);
// 回溯
sum -= candidates[i];
path.removeLast();
}
}
}总结
排序 + 剪枝是常见的套路
40.⭐ 组合总和 II
本题开始涉及到一个问题了:去重。
注意题目中给我们 集合是有重复元素的,那么求出来的 组合有可能重复,但题目要求不能有重复组合。
题目链接:https://leetcode.cn/problems/combination-sum-ii
文章讲解:https://programmercarl.com/0040.组合总和II.html
视频讲解:https://www.bilibili.com/video/BV12V4y1V73A
思路分析
本题的几个注意点
(1)给定的数组,包含重复元素,需要去重操作
(2)每个数字在每个组合中只能使用一次,但是同一个组合可以出现重复元素(是不同的元素,只是他们的值相同而已)
(3)解集不能包含重复的组合
⚠️ 剪枝分析
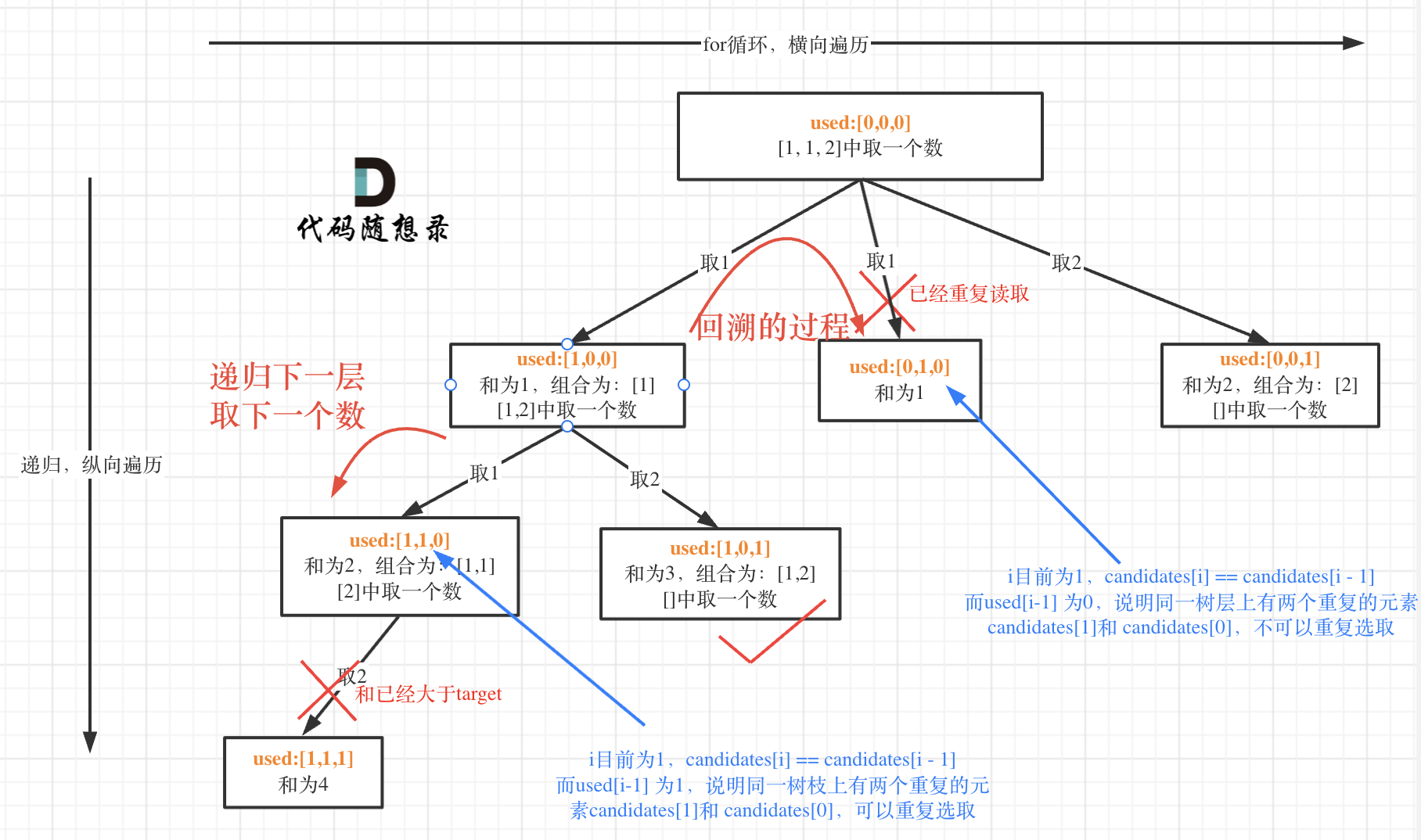
首先给定的数组中存在重复元素,需要考虑组合的过程中结果可能出现重复的组合(需要树层去重),但是同一个组合中的元素可以重复(不同元素,但是值相同)
去重逻辑的具体说明
为什么同一组合的元素无需去重?
在上图中,树层上第一次选取了 1 ,之后递归选取,这个时候如果出现元素重复,选取的是不同的元素,但是他们的值相同
树层上第一次选取了 1,递归层选取元素组合是在除了第一次选取的 1 的基础上选取的(即包含在第二次选取的 1 之后,递归时寻找组合需要的元素),之后得到符合条件的组合
为什么第二次选取 1 需要去重?(树层去重)
因为第一次选取了 1 在递归的时候选取的元素包含第二次选取的 1 之后的元素,则第二次选取了 1 之后,再递归时找到符合条件的组合必定是第一次选取了 1 递归时候找到符合条件的组合的子集,即结果集的元素组合出现重复,需要去重处理
采用标记数组的说明
如果 candidates[i] == candidates[i - 1] 并且 used[i - 1] == false,就说明:前一个树枝,使用了 candidates[i - 1],也就是说同一树层使用过 candidates[i - 1]
used[i - 1] == true,说明同一树枝 candidates[i - 1]使用过
used[i - 1] == false,说明同一树层 candidates[i - 1]使用过
为什么 used[i - 1] == false 就是同一树层呢?
简单理解:注意代码中回溯的逻辑,如果使用过会置为 true,但是回溯会置为 false,即 false 的结果是通过回溯得来的,说明之前已经使用过
具体解释
(1)因为同一树层,used[i - 1] == false 才能表示,当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的
(2)而 used[i - 1] == true,说明是进入下一层递归,取下一个数,所以是树枝上
总结
求排列(元素位置有关) ➜ 用 used[]
求子集/组合(元素位置无关) ➜ 用 i > startIndex
题解(startIndex 去重)
java
class Solution {
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates); // 排序的目的是去重 + 剪枝
backtracking(candidates,target,0,0);
return res;
}
public void backtracking(int[] candidates, int target, int sum, int startIndex) {
if (sum > target) {
return;
}
if (sum == target) {
res.add(new ArrayList<>(path));
return;
}
for (int i = startIndex; i < candidates.length; i++) {
// 剪枝
if (sum + candidates[i] > target) {
break;
}
// 树层去重,i > startIndex 是为了防止下标越界,确保 i - 1 >= 0
if (i > startIndex && candidates[i - 1] == candidates[i]) {
continue;
}
path.add(candidates[i]);
sum += candidates[i];
// 递归
backtracking(candidates,target,sum,i + 1); // 每个数字在每个组合中只能使用一次
// 回溯
path.removeLast();
sum -= candidates[i];
}
}
}题解(标记数组去重)
java
class Solution {
LinkedList<Integer> path = new LinkedList<>();
List<List<Integer>> ans = new ArrayList<>();
boolean[] used;
int sum = 0;
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
used = new boolean[candidates.length];
// 加标记数组,用来辅助判断同层节点是否已经遍历
Arrays.fill(used, false); // 初始化全部值为 false
// 排序得目的是为了将相同得元素挨在一起,方便去重,
// 因为去重是根据 used[i- 1] == false 来判断的
backTracking(candidates, target, 0);
return ans;
}
private void backTracking(int[] candidates, int target, int startIndex) {
if (sum == target) {
ans.add(new ArrayList(path));
}
for (int i = startIndex; i < candidates.length; i++) {
if (sum + candidates[i] > target) {
break;
}
/*
(1) i > 0 是为了防止下标越界,确保 i - 1 >= 0
(2)若出现了两个一样的元素,used[i - 1] == false 说明第一个元素
在前一次递归中使用过,通过回溯操作才使得 used[i - 1] == false,
第一个元素递归是形成的组合已经包含了第二个元素在递归时形成的组合,
因为两个元素相同,且元素不能重复使用,则遇到第二个相同元素时需要去重
*/
if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
continue;
}
used[i] = true;
sum += candidates[i];
path.add(candidates[i]);
// 每个节点仅能选择一次,所以从下一位开始
backTracking(candidates, target, i + 1);
used[i] = false;
sum -= candidates[i];
path.removeLast();
}
}
}总结
去重一定要排序,又是一个常见套路
131.分割回文串
本题较难,大家先看视频来理解 分割问题,明天还会有一道分割问题,先打打基础。
题目链接:https://leetcode.cn/problems/palindrome-partitioning/description
文章讲解:https://programmercarl.com/0131.分割回文串.html
视频讲解:https://www.bilibili.com/video/BV1c54y1e7k6
思路分析
两个问题
(1)如何切割字串
(2)如何判断是否是回文串
与组合问题的相似点
例如:对于字符串 abcdef
组合问题:选取一个 a 之后,在 bcdef 中再去选取第二个,选取 b 之后在 cdef 中再选取第三个.....
切割问题:切割一个 a 之后,在 bcdef 中再去切割第二段,切割 b 之后在 cdef 中再切割第三段.....
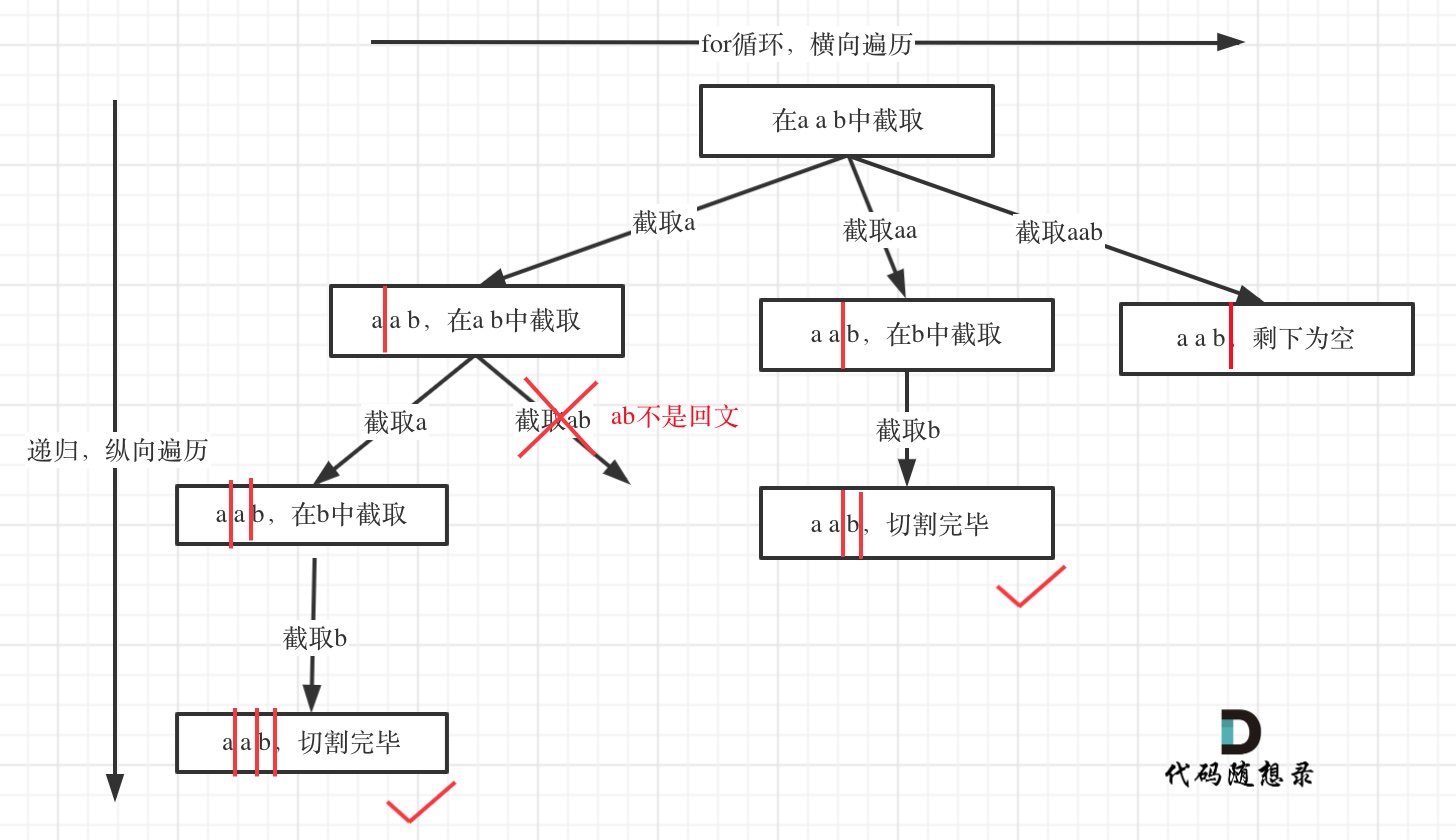
如何实现切割字串呢?
定义了 for 循环,i 在不断递增,然而 startIndex 的递增是有条件的,那[startIndex,i]这个区间就是截取的字串,而 startIndex 就是切割线
题解
java
class Solution {
List<List<String>> res = new ArrayList<>();
List<String> cur = new ArrayList<>();
public List<List<String>> partition(String s) {
backtracking(s, 0);
return res;
}
public void backtracking(String s, int startIndex) {
// startIndex 就是分割线,当切割到末尾就结束了
if (startIndex == s.length()) {
res.add(new ArrayList<>(cur));
return;
}
for (int i = startIndex; i < s.length(); i++) {
/*
1. startIndex是切割线,截取字串,判断是否是回文串
2. substring()方法左闭右开,注意 + 1
*/
String str = s.substring(startIndex, i + 1);
if (isPalindrome(str)) {
cur.add(str);
/* 注意切割过的位置,不能重复切割,所以,backtracking(s, i + 1);
传入下一层的起始位置为i + 1
*/
backtracking(s, i + 1);
cur.remove(cur.size() - 1); // 回溯
}
}
}
// 判断是否是回文串
public boolean isPalindrome(String sb) {
for (int i = 0, j = sb.length() - 1; i < sb.length(); i++, j--) {
if (sb.charAt(i) != sb.charAt(j)) {
return false;
}
}
return true;
}
}