Day 48

---

108.冗余连接

并查集应用类题目，关键是如何把题意转化成并查集问题

题目链接：https://kamacoder.com/problempage.php?pid=1181

文章讲解：https://www.programmercarl.com/kamacoder/0108.冗余连接.html

视频讲解：https://www.bilibili.com/video/BV1gRM3z9EwZ

思路分析

使用并查集解决，逐次加入每一组边，如果发现新加入的边已经在集合中了，则说明是冗余边

题解

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int pointNUm  = scanner.nextInt();
        DisJoint disJoint = new DisJoint(pointNUm);
        for (int i = 0; i < pointNUm; i++) {
            disJoint.join(scanner.nextInt(), scanner.nextInt());
        }
    }
}

class DisJoint {
    private int[] father;

    public DisJoint(int N) {
        // N 个节点有 N - 1 条边
        father = new int[N + 1];
        // 初始时指向自己
        for (int i = 1; i < N; i++) {
            father[i] = i;
        }
    }

    public int find(int n) {
        // 找到了根节点，返回
        if (n == father[n]) {
            return n;
        }
        // 路径压缩
        return father[n] = find(father[n]);
    }

    public void join(int n, int m) {
        int rootN = find(n);
        int rootM = find(m);

        // 判断是否已经在同一个集合中，避免重复添加
        if (rootN == rootM) {
            // 如果已经在同一个集合中，输出（只输出一次）
            System.out.println(n + " " + m);
            return;
        }

        // 合并两个集合，按根节点合并
        father[rootN] = rootM;
    }

    public boolean isSame(int n, int m) {
        n = find(n);
        m = find(m);
        return m == n;
    }
}

⚠️ 109.冗余连接 II

上面两道题目是不是感觉做出自信了，感觉并查集不过如此？ 来这道题目 给大家适当一些打击， 难度上来了。

题目链接：https://kamacoder.com/problempage.php?pid=1182

文章讲解：https://www.programmercarl.com/kamacoder/0109.冗余连接II.html

视频讲解：https://www.bilibili.com/video/BV1t2NEzaEMR

思路分析

本题从无向图转为了有向图，寻找冗余边的突破点就是寻找入度为 2 的节点

本题的本质是 ：有一个有向图，由一颗有向树 + 一条冗余的有向边组成，需要找到那条冗余的边，把这条边删了，让这个图恢复为有向树

三大情况

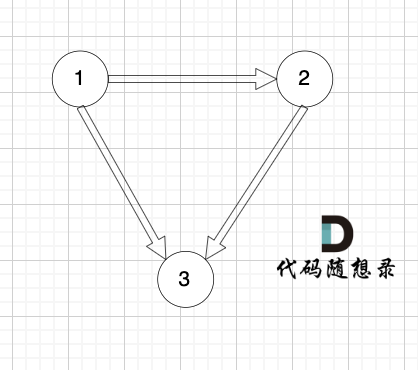
（1）情况一：如果我们找到入度为 2 的点，那么删一条指向该节点的边就行了

（2）情况二：只能删特定的一条边

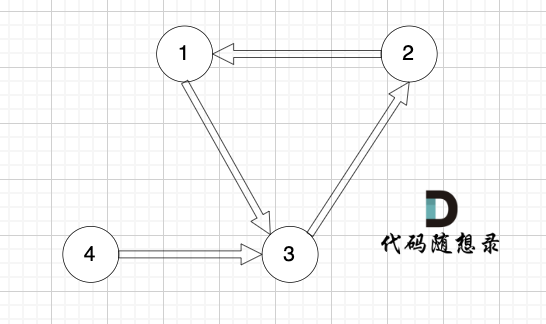
节点 3 的入度为 2，但在删除边的时候，只能删除由节点 1 -> 节点 3 的这条边，如果删除由节点 4 -> 节点 3 的这条边，此时就变成情况一了，成环了，删除边并不能达到恢复为有向树的目的

（3）情况三： 如果没有入度为 2 的点，说明图中有环了（注意是有向环）

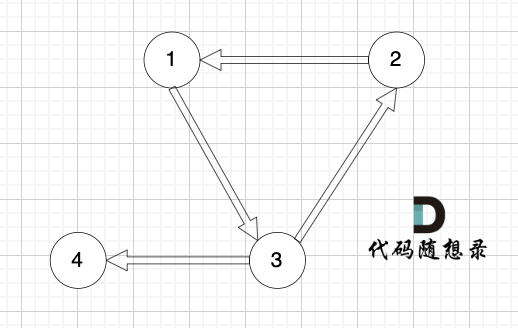
对于情况三，删掉构成环的边就可以了

题解

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class Main {

    static class Disjoint {
        private final int[] father;

        public Disjoint(int n) {
            father = new int[n + 1];
            for (int i = 1; i <= n; i++) {
                // 初始时指向自己
                father[i] = i;
            }
        }

        public void join(int n, int m) {
            // 首先判断是否在同一集合中
            m = find(m);
            n = find(n);
            if (m == n) {
                return;
            }
            father[n] = m;
        }

        public int find(int n) {
            // 找到了根节点
            if (n == father[n]) {
                return n;
            }
            return father[n] = find(father[n]);
        }

        public boolean isSame(int n, int m) {
            m = find(m);
            n = find(n);
            return m == n;
        }
    }

    static class Edge {
        int s;
        int t;

        public Edge(int s, int t) {
            this.s = s;
            this.t = t;
        }
    }

    static class Node {
        int in;
        int out;
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        List<Edge> edges = new ArrayList<>();
        // 节点编号从 1 开始，记录每一个节点的入度和出度
        Node[] nodeMap = new Node[n + 1];
        for (int i = 1; i <= n; i++) {
            nodeMap[i] = new Node();
        }
        Integer doubleIn = null;
        for (int i = 0; i < n; i++) {
            int s = scanner.nextInt();
            int t = scanner.nextInt();
            // 统计入度
            nodeMap[t].in++;
            // 找到了入度大于 2 的节点，记录该节点
            if (!(nodeMap[t].in < 2)) {
                doubleIn = t;
            }
            // 加入边
            Edge edge = new Edge(s, t);
            edges.add(edge);
        }

        // 定义冗余边
        Edge result = null;

        // 存在入度为 2 的节点
        if (doubleIn != null) {
            // 记录两条入度边
            List<Edge> doubleInEdges = new ArrayList<>();
            for (Edge edge : edges) {
                // 遍历所有边，找到入度为 2 的节点的两条入度边
                if (edge.t == doubleIn) {
                    doubleInEdges.add(edge);
                }
            }

            // 找到两条入度边后，优先处理后面那一条边
            Edge edge = doubleInEdges.get(1);

            // 情况一：存在入度为 2 的节点，删除该边后是有向树
            if (isTreeWithExclude(edges, nodeMap, edge)) {
                result = edge;
            }else { // 情况二：存在入度为 2 的节点，删除该边后，无法形成有向树，则删除前面那条边
                result = doubleInEdges.get(0);
            }
        } else {
            // 情况三：不存在入度为 2 的节点，解除环即可（用并查集找冗余的边）
            result = getRemoveEdge(edges, nodeMap);
        }
        // 通过边找到链接的两个节点
        System.out.println(result.s + " " + result.t);
    }

    public static boolean isTreeWithExclude(List<Edge> edges, Node[] nodeMap, Edge excludeEdge) {
        Disjoint disjoint = new Disjoint(nodeMap.length);
        for (Edge edge : edges){
            // 如果遍历到需要删除的边，则不做处理，交给删除边的方法处理
            if (edge == excludeEdge){
                continue;
            }
            // 成环则不是树
            if (disjoint.isSame(edge.s,edge.t)){
                return false;
            }
            // 两个节点不在一个集合中，则加入并查集
            disjoint.join(edge.s,edge.t);
        }
        // 如果不处理删除的边，并且其余边不会构成环（并查集判断），说明就是有向树
        return true;
    }

    // 运用并查集的思路找冗余边
    public static Edge getRemoveEdge(List<Edge> edges, Node[] nodeMap) {
        int length = nodeMap.length;
        Disjoint disjoint = new Disjoint(length);

        for (Edge edge : edges){
            // 在同一个集合中则说明是冗余边
            if (disjoint.isSame(edge.s,edge.t)){
                return edge;
            }
            // 否则说明不在同一个集合中，加入并查集
            disjoint.join(edge.s,edge.t);
        }
        return null;
    }
}