Day 2
209.长度最小的子数组
题目建议: 本题关键在于理解滑动窗口,拓展题目可以先不做。
题目链接:https://leetcode.cn/problems/minimum-size-subarray-sum/
文章讲解:https://programmercarl.com/0209.长度最小的子数组.html
视频讲解:https://www.bilibili.com/video/BV1tZ4y1q7XE
(1)滑动窗口
滑动窗口的本质:双指针
滑动窗口的精髓:窗口的起始位置如何移动
(2)基本介绍
窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。
窗口的起始位置如何移动:如果当前窗口的值大于等于 s 了,窗口就要向前移动了(也就是该缩小了)。
窗口的结束位置如何移动:窗口的结束位置就是遍历数组的指针,也就是 for 循环里的索引。
public class Solution {
// 滑动窗口(双指针)
public int minSubArrayLen(int target, int[] nums) {
int i = 0;
int sum = 0;
int min_length = Integer.MAX_VALUE;
for (int j = 0; j < nums.length; j++) {
// 计算和
sum += nums[j];
// 在滑动过程中持续判断
while (sum >= target) {
min_length = Math.min(min_length, j - i + 1); // 取最小长度
sum -= nums[i]; // 头指针前移一位,区间和需要减去头指针指向的值
i++;
}
}
return min_length == Integer.MAX_VALUE ? 0 : min_length;
}
}代码分析
- 首先通过循环,让位置开始移动,依次遍历找到符合条件的窗口长度
- 如果找到了符合条件的长度
- 首先记录当前窗口的长度:j - i + 1
- 通过函数找到窗口的最小长度,在后续循环中不断更新(使用 while 循环)
- 让头指针前移一位,同时更新窗口的和(容易遗漏)
- 注意:在题目中要求(如果不存在符合条件的子数组,返回 0 ),最后返回值的处理需要注意
(3)补充题目
59.螺旋矩阵 II
题目建议: 本题关键还是在转圈的逻辑
题目链接:https://leetcode.cn/problems/spiral-matrix-ii/
文章讲解:https://programmercarl.com/0059.螺旋矩阵II.html
视频讲解:https://www.bilibili.com/video/BV1SL4y1N7mV/
(1)思路分析
本题的关键:遍历的区间长度如何选择?
这里采用二分法中左闭右开的思路,最后一个点由下一次遍历处理
解题步骤
- 首先通过模拟,实现四个方向的模拟,同时在矩阵中填入数据
- 圈数
- 关系-->圈数 = n / 2
- 偶数圈:圈数刚好是整数,模拟完四个方向即可
- 奇数圈:单独处理最后一个点
关键点:理解遍历终点的位置和边界的关系
(2)题解
public class Solution {
public int[][] generateMatrix(int n) {
// 核心思想在左闭右开,该条边的最后一个点由下一条边处理
int[][] nums = new int[n][n]; // 矩阵的初始化
int start_x = 0, start_y = 0; // 每一圈的起点
int i, j; // i 代表行,j 代表列
int loop = 1; // 记录圈数
int count = 1; // 矩阵中填入的数字
int offset = 1;
while (loop <= n / 2) {
// 向右走
for (j = start_y; j < n - offset; j++) {
nums[start_x][j] = count;
count++;
}
// 向下走
for (i = start_x; i < n - offset; i++) {
nums[i][j] = count;
count++;
}
// 向左走
for (; j > start_y; j--) {
nums[i][j] = count;
count++;
}
// 向上走
for (; i > start_x; i--) {
nums[i][j] = count;
count++;
}
// 一圈结束后,变化起始坐标
start_x++;
start_y++;
offset++; // 往里走了一圈,终点位置往里缩小,差值增大
loop++; // 圈数自增一
}
// 处理奇数圈最后一个点
if(n % 2 == 1){
nums[start_x][start_y] = count;
}
return nums;
}
}代码分析
- 定义好变量,通过 offset 来控制遍历的终点
- 每一圈结束后,进入内圈
- 起始点坐标变化
- 终点位置减小,offset 值需要自增
- 圈数自增
- 根据思路,模拟四个方向的遍历,最后再单独处理奇数圈中的最后一个点
区间和
题目建议:掌握前缀和思想
文章讲解:https://www.programmercarl.com/kamacoder/0058.区间和.html
(1)一维前缀和介绍
场景引出:给定一个一维数组,给出任意区间,要求求改区间的和
常规思路:使用循环遍历,对该区间求和即可
常规思路带来的问题是什么?
如果查询 m 次,每次查询的范围都是从 0 到 n - 1,那么该算法的时间复杂度是 O(n * m) m 是查询的次数,如果查询次数非常大的话,这个时间复杂度也是非常大的。
前缀和的优点:前缀和的思想是重复利用计算过的子数组之和,从而降低区间查询需要累加计算的次数
前缀和方法介绍
- 原始数组 vec[]
- 前缀和数组 p[]:记录从 vec[0]--->vec[i]的和
- 区间[a,b]的和:sum[a,b] = p[b] - p[a - 1]
图解分析
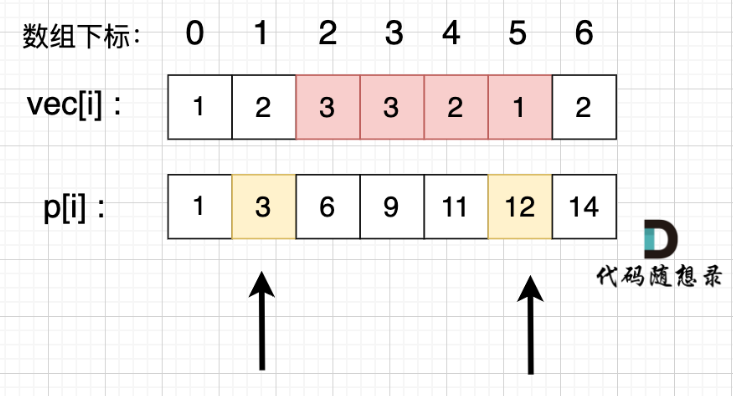
(2)题解
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int vec[] = new int[n];
int[] p = new int[n]; // 前缀和数组
int presum = 0;
for (int i = 0; i < n; i++) {
vec[i] = scanner.nextInt();
presum += vec[i];
p[i] = presum; // 初始化前缀和数组
}
// 循环读取整数,每一轮读取两个,表示区间和的范围
while(scanner.hasNextInt()){
int a = scanner.nextInt();
int b = scanner.nextInt();
int sum;
if(a==0){ // 判断左端点是为 0
sum = p[b];
}else{
sum = p[b] - p[a - 1];
}
System.out.println(sum);
}
scanner.close();
}
}代码分析
- 前缀和数组的初始化:初始化原始数组的同时计算前缀和
- 判断前缀和的左区间是否为 0
- 左区间为 0:前缀和 = p[b]的值
- 左区间不为 0:前缀和 = p[b] - p[a - 1](不理解可以看前面的图解)
补充:循环条件 scanner.hasNextInt() 表示的循环读入整数,在每一轮循环中读入两个整数
开发商购买土地
题目建议:本题是一维前缀和的应用,知识点延伸:二维前缀和
https://www.programmercarl.com/kamacoder/0044.开发商购买土地.html
(1)一维前缀和应用
思路分析
- 如果使用循环暴力破解,时间复杂度会很大,不推荐
- 由于题目要求求的是总和,这里可以采用一位前缀和的思想,对每一行,每一列求和,在后续中直接查找前缀和求差值即可
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int sum = 0; // 统计总和
int[][] vec = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
vec[i][j] = scanner.nextInt();
sum += vec[i][j];
}
}
// 统计横向和
int[] horizontal = new int[n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
horizontal[i] += vec[i][j];
}
}
// 统计纵向和
int[] vertical = new int[m];
for (int j = 0; j < m; j++) {
for (int i = 0; i < n; i++) {
vertical[j] += vec[i][j];
}
}
int result = Integer.MAX_VALUE;
// 横向切割,找出最小的总和差值
int horizontalCut = 0;
for (int i = 0; i < n; i++) {
horizontalCut += horizontal[i]; // 取前缀和
// 利用总和求另一部分的和
result = Math.min(result,Math.abs((sum - horizontalCut) - horizontalCut));
}
// 纵向切割,找出最小的总和差值
int verticalCut = 0;
for (int j = 0; j < m; j++) {
verticalCut += vertical[j];
// 利用总和求另一部分的和
result = Math.min(result,Math.abs((sum - verticalCut) - verticalCut));
}
System.out.println(result);
scanner.close();
}
}代码分析
- 首先初始化二维矩阵,并求出矩阵的和(在后续可以使用差值计算另一半矩阵的和)
- 之后通过横向和纵向切分,分别计算每一行和每一列的前缀和,保存到数组中
- 使用循环对行和列切割,使用函数依次计算最小的差值,并在下一次循环中更新
- 输出最小的差值,关闭 scanner,避免资源的浪费
(2)二维前缀和
本题是在一维前缀和的视角下解决的。但是题目本身是二维矩阵特点,我们可以引出二维前缀和
1. 基本介绍
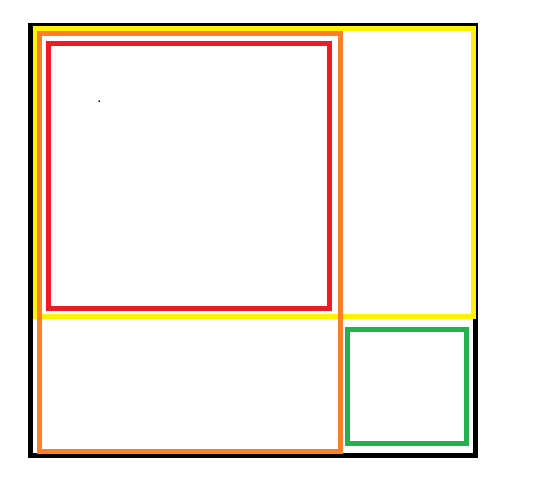
矩形的说明
- 我们将一个矩形划分成了不同的区域
- 整个矩形:黑色方框
- 左边的矩形:橙色方框
- 上面的矩形:黄色方框
- 左上角的矩形:红色方框
- 右下角的矩形:绿色方框
- 关系:整个矩形(黑色方框) = 橙色区域 + 黄色区域 - 红色区域 + 蓝色区域
2. 定义
说明:二维矩阵的起始坐标为(1,1),不采用(0,0),目的是为了方便处理
二维前缀和中,s[i][j] 表示以 s[1][1]为左上角顶点,s[i][j]为右下角顶点,两个顶点作为对角线构成的矩形中元素的和
3. 推导图解矩形的公式(二维前缀和的构建)
首先明确 sum [i][j]的定义,根据各部分矩形的和可以得到如下公式
公式:sum [i][j]=sum [i-1][j]+sum [i][j-1]-sum [i-1][j-1]+a [i][j]
- sum [i][j]:黑色方框
- sum [i-1][j]:黄色方框
- sum [i][j-1]:橙色方框
- sum [i-1][j-1]:红色方框(黄色方框和橙色方框重叠的部分,需要减掉)
- a [i][j]:绿色方框
- 推导绿色方框:a [i][j] = sum [i][j] - sum [i-1][j] - sum [i][j-1] + sum [i-1][j-1]
对该公式进行抽象:绿色方框看作就是我们任意的子矩阵,该面积可以有上诉公式的来
4. 公式(二维前缀和的查询)
公式来由:根据图解矩阵中的公式逆推求解绿色方框的和,通过抽象得到
若以(a,b)为左上角,(c,d)为右下角,则任意子矩阵的和为sum[c][d] - sum[a-1][b] - sum[a][b-1] + sum[a-1][b-1]
5. 公式总结
(1)构建二维前缀和
sum [i][j]=sum [i-1][j]+sum [i][j-1]-sum [i-1][j-1]+a [i][j](2)查询二位前缀和
a [i][j] = sum [i][j] - sum [i-1][j] - sum [i][j-1] + sum [i-1][j-1](3)二维前缀和应用
注意点:二维矩阵的初值为 a[1][1],不用 0 作为初始值
二维矩阵题解如下
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] s = new int[n + 1][m + 1]; // 前缀和数组
int result = Integer.MAX_VALUE;
// 通过二维前缀和的定义,构建前缀和
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
int x = scanner.nextInt();
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + x;
}
}
// 行切割
for (int i = 1; i < n; i++) {
int ans = Math.abs((s[n][m] - s[i][m]) - s[i][m]);
result = Math.min(result, ans);
}
// 列切割
for (int j = 1; j < m; j++) {
int ans = Math.abs((s[n][m] - s[n][j]) - s[n][j]);
result = Math.min(result, ans);
}
System.out.println(result);
scanner.close();
}
}代码分析
- 通过前面的推导,使用公式构建二维前缀和
- 通过行切割,列切割,计算最小的差值,
- 输出最小的差值,关闭 scanner
总结
- 滑动窗口:理解滑动的原理和头指针什么时候移动
- 矩阵的模拟:关键在于边界的处理(左闭右开)
- 前缀和
- 一维前缀和
- 二维前缀和
