位运算实现加减乘除
题目链接
https://leetcode.cn/problems/divide-two-integers/
加法实现
思路分析
两数相加可以等价为无进位相加的结果 + 进位信息
如果发生进位,则两位必定为 1,可以通过 a & b 保留所有位都为 1 的信息,而这些位就是进位信息
进位信息是进到了上一位,所以得到的进位信息需要左移一位
代码实现
java
public static int add(int a, int b) {
int ans = a;
while (b != 0) {
// ans : a 和 b 无进位相加的结果
ans = a ^ b;
// b : a 和 b 相加时的进位信息
b = (a & b) << 1;
// 得到了两个信息,答案是 ans + b
// 而此时又是相加操作,复用前面的过程即可
// 相当于又执行 a + b,将 ans 的值给 a
a = ans;
}
// 如果 b 为 0,返回 a,即为 ans
// 如果进位信息(b)消失了,则最后就是 a + b 的答案,返回 ans
return ans;
}减法实现
思路分析
减法的本质还是加法:a - b <---> a + (-b)
一个数的相反数在二进制运算中的实现为:取反 + 1,通过加法实现
代码实现
java
public static int minus(int a, int b) {
return add(a, neg(b));
}
public static int neg(int n) {
return add(~n, 1);
}乘法实现
思路分析
这里是模拟数学运算的乘法逻辑,对于 a * b,若 b 每一位乘 a 不为 0,则最后是需要累加结果的,累加的结果应该是在对应的位上相乘得到的,具体入下图
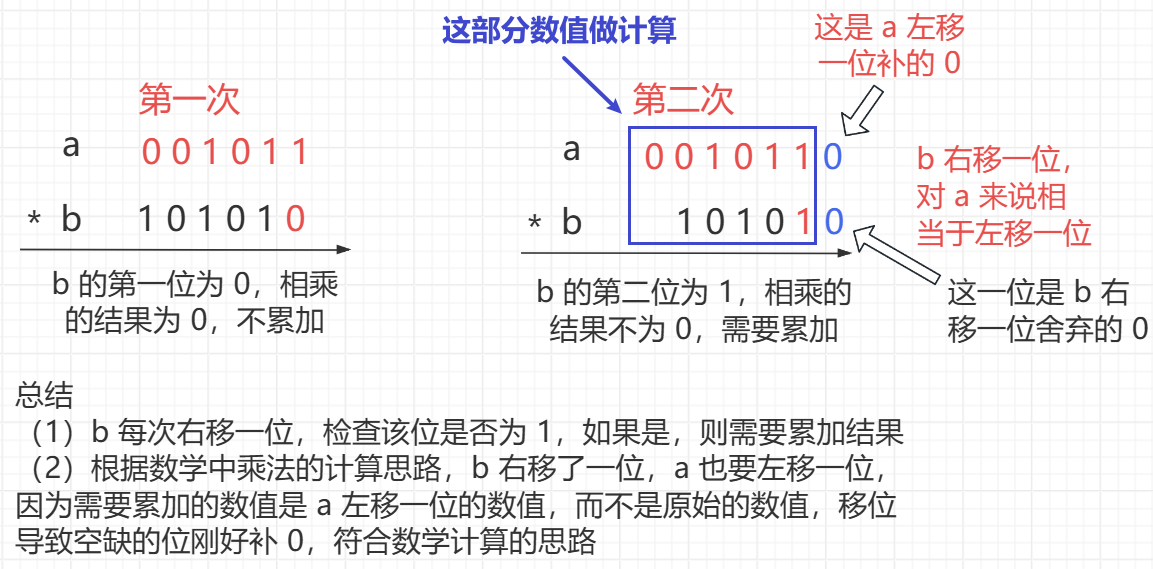
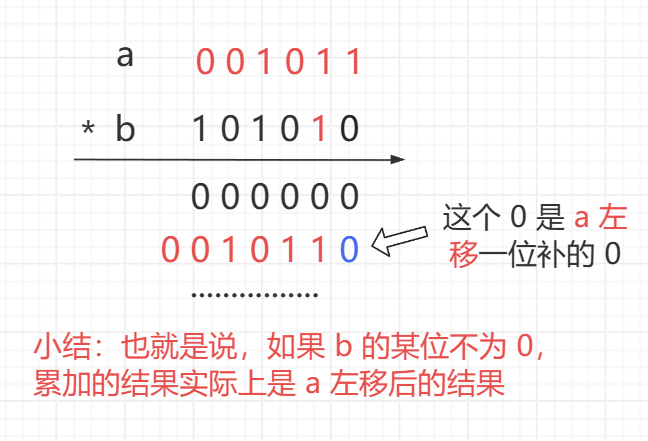
代码实现
java
// 这种乘法后面有大用处,尤其是求(a 的 b 次方 % m)的结果,也叫龟速乘
public static int multiply(int a, int b) {
// 说明:只要 a * b 的结果不溢出,无论整数还是负数,最后的结果总是可以计算正确
int ans = 0;
while (b != 0) {
// 检查 b 的二进位状态,只要不为 0,就累加结果
// 累加的结果是 b 左移后的结果
if ((b & 1) != 0) {
ans = add(ans, a);
}
// a,b 同时移动,如果 b 的二进制位不为 0,才能保证累加的结果才嫩正确
// 如果不理解,可以使用数学乘法的思路计算二进制数的乘法体会
a <<= 1;
b >>>= 1;
}
return ans;
}除法实现
思路分析
前提:对于非负的 a、b,且 a、b 都不是整数最大或者最小,a / b 可以等价于以下形式(注意结果是向下取整的)
280 / 25 = 25 * 23 + 25 * 21 + 25 * 20 + 5,因为结果向下取整,余数可以忽略
280 / 25 = 25 * (23 + 21 + 20),后面这部分不就是二进制转十进制的计算方法,于是可以得到相除结果的二进制
依据上述思路,若 a / b,可以从 230 开始,依次递减,每次判断 a 是否大于等于 b * 2 i,如果符合,就把对应的二进制设置为 1
由于 b * 2 i 是通过左移实现的,考虑到溢出的风险,等价写法是 a 右移 i 与 b 进行比较,如果 a 右移 i 位大于等于 b,则下一轮判断更新 a = a - b * 2 i
等价关系:a 是否大于 b * 2 i ---> a / 2 i 是否大于 b ---> a 右移 i 位是否大于 b
非负且不是最大最小
java
// 必须保证 a 和 b 都不是整数最小值,返回 a 除以 b 的结果
public static int div(int a, int b) {
// neg 方法返回相反数:取反 + 1
// 如果小于 0,就先处理成大于 0
int x = a < 0 ? neg(a) : a;
int y = b < 0 ? neg(b) : b;
int ans = 0;
// 一共 32 位(0 - 31),忽略符号位,从 30 开始
// 不能体现算术运算,这里 i-- 调用 minus 方法实现
for (int i = 30; i >= 0; i = minus(i, 1)) {
// 每次判断 x 是否大于等于 y * 2 的 i 次方
// 考虑到溢出风险,以下为等价写法
if ((x >> i) >= y) {
ans |= (1 << i);
x = minus(x, y << i);
}
}
// 符号不一样,异或结果为 1,最后的结果应为相除结果的相反数
return a < 0 ^ b < 0 ? neg(ans) : ans;
}特殊情况处理
java
public static int divide(int a, int b) {
// a、b 都是整数最小,返回 1
if (a == MIN && b == MIN) {
return 1;
}
// a 和 b 都不是整数最小,那么正常去除
if (a != MIN && b != MIN) {
return div(a, b);
}
// a 不是整数最小,b 是整数最小,结果为 0
// 可以把负号提出来,a / b(无限大)的结果趋近于 0
// a / b 的结果是向下取整的,即 -0.000....向下取整为 0
if (b == MIN) {
return 0;
}
// a 是整数最小,b是 -1,返回整数最大,因为题目里明确这么说了
if (b == neg(1)) {
return Integer.MAX_VALUE;
}
// a 是整数最小,b 不是整数最小,b也不是 -1
// 分 b > 0 和 b < 0 两种情况套路最后的结果正负
// 因为 a 是整数最小,在二进制中没有与之对应的正数,需要特殊处理
// 如果 b > 0,加上 b 没有这么小了,可以使用 divide 方法
// 因为 (a + b)/ b = (a / b) + 1,所以最后还要 -1
// 如果 b < 0,减去 b 没有这么小了,可以使用 divide 方法
// 因为 (a -(- b))/ b = (a + b)/ b = (a / b) + 1,所以最后还要 +1
a = add(a, b > 0 ? b : neg(b));
int ans = div(a, b);
int offset = b > 0 ? neg(1) : 1;
return add(ans, offset);
}完整代码
java
// 必须保证 a 和 b 都不是整数最小值,返回 a 除以 b 的结果
public static int div(int a, int b) {
// neg 方法返回相反数:取反 + 1
// 如果小于 0,就先处理成大于 0
int x = a < 0 ? neg(a) : a;
int y = b < 0 ? neg(b) : b;
int ans = 0;
// 一共 32 位(0 - 31),忽略符号位,从 30 开始
// 不能体现算术运算,这里 i-- 调用 minus 方法实现
for (int i = 30; i >= 0; i = minus(i, 1)) {
// 每次判断 x 是否大于等于 y * 2 的 i 次方
// 考虑到溢出风险,以下为等价写法
if ((x >> i) >= y) {
ans |= (1 << i);
x = minus(x, y << i);
}
}
// 符号不一样,异或结果为 1,最后的结果应为相除结果的相反数
return a < 0 ^ b < 0 ? neg(ans) : ans;
}
public static int divide(int a, int b) {
// a、b 都是整数最小,返回 1
if (a == MIN && b == MIN) {
return 1;
}
// a 和 b 都不是整数最小,那么正常去除
if (a != MIN && b != MIN) {
return div(a, b);
}
// a 不是整数最小,b 是整数最小,结果为 0
// 可以把负号提出来,a / b(无限大)的结果趋近于 0
// a / b 的结果是向下取整的,即 -0.000....向下取整为 0
if (b == MIN) {
return 0;
}
// a 是整数最小,b是 -1,返回整数最大,因为题目里明确这么说了
if (b == neg(1)) {
return Integer.MAX_VALUE;
}
// a 是整数最小,b 不是整数最小,b也不是 -1
// 分 b > 0 和 b < 0 两种情况套路最后的结果正负
// 因为 a 是整数最小,在二进制中没有与之对应的正数,需要特殊处理
// 如果 b > 0,加上 b 没有这么小了,可以使用 divide 方法
// 因为 (a + b)/ b = (a / b) + 1,所以最后还要 -1
// 如果 b < 0,加上 -b 没有这么小了(-b > 0),可以使用 divide 方法
// 因为 (a +(- b))/ b = (a - b)/ b = (a / b) - 1,所以最后还要 +1
a = add(a, b > 0 ? b : neg(b));
int ans = div(a, b);
int offset = b > 0 ? neg(1) : 1;
return add(ans, offset);
}代码实现
java
class Solution {
public static int MIN = Integer.MIN_VALUE;
public static int divide(int a, int b) {
// a、b 都是整数最小,返回 1
if (a == MIN && b == MIN) {
return 1;
}
// a 和 b 都不是整数最小,那么正常去除
if (a != MIN && b != MIN) {
return div(a, b);
}
// a 不是整数最小,b 是整数最小,结果为 0
// 可以把负号提出来,a / b(无限大)的结果趋近于 0
// a / b 的结果是向下取整的,即 -0.000....向下取整为 0
if (b == MIN) {
return 0;
}
// a 是整数最小,b是 -1,返回整数最大,因为题目里明确这么说了
if (b == neg(1)) {
return Integer.MAX_VALUE;
}
// a 是整数最小,b 不是整数最小,b也不是 -1
// 分 b > 0 和 b < 0 两种情况套路最后的结果正负
// 因为 a 是整数最小,在二进制中没有与之对应的正数,需要特殊处理
// 如果 b > 0,加上 b 没有这么小了,可以使用 divide 方法
// 因为 (a + b)/ b = (a / b) + 1,所以最后还要 -1
// 如果 b < 0,减去 b 没有这么小了,可以使用 divide 方法
// 因为 (a -(- b))/ b = (a + b)/ b = (a / b) + 1,所以最后还要 +1
a = add(a, b > 0 ? b : neg(b));
int ans = div(a, b);
int offset = b > 0 ? neg(1) : 1;
return add(ans, offset);
}
// 必须保证 a 和 b 都不是整数最小值,返回 a 除以 b 的结果
public static int div(int a, int b) {
// neg 方法返回相反数:取反 + 1
// 如果小于 0,就先处理成大于 0
int x = a < 0 ? neg(a) : a;
int y = b < 0 ? neg(b) : b;
int ans = 0;
// 一共 32 位(0 - 31),忽略符号位,从 30 开始
// 不能体现算术运算,这里 i-- 调用 minus 方法实现
for (int i = 30; i >= 0; i = minus(i, 1)) {
// 每次判断 x 是否大于等于 y * 2 的 i 次方
// 考虑到溢出风险,以下为等价写法
if ((x >> i) >= y) {
ans |= (1 << i);
x = minus(x, y << i);
}
}
// 符号不一样,异或结果为 1,最后的结果应为相除结果的相反数
return a < 0 ^ b < 0 ? neg(ans) : ans;
}
public static int add(int a, int b) {
int ans = a;
while (b != 0) {
// ans : a 和 b 无进位相加的结果
ans = a ^ b;
// b : a 和 b 相加时的进位信息
b = (a & b) << 1;
// 得到了两个信息,答案是 ans + b
// 而此时又是相加操作,复用前面的过程即可
// 相当于又执行 a + b,将 ans 的值给 a
a = ans;
}
// 如果 b 为 0,返回 a,即为 ans
// 如果进位信息(b)消失了,则最后就是 a + b 的答案,返回 ans
return ans;
}
public static int minus(int a, int b) {
return add(a, neg(b));
}
public static int neg(int n) {
return add(~n, 1);
}
// 这种乘法后面有大用处,尤其是求(a 的 b 次方 % m)的结果,也叫龟速乘
public static int multiply(int a, int b) {
// 说明:只要 a * b 的结果不溢出,无论整数还是负数,最后的结果总是可以计算正确
int ans = 0;
while (b != 0) {
// 检查 b 的二进位状态,只要不为 0,就累加结果
// 累加的结果是 b 左移后的结果
if ((b & 1) != 0) {
ans = add(ans, a);
}
// a,b 同时移动,如果 b 的二进制位不为 0,才能保证累加的结果才嫩正确
// 如果不理解,可以使用数学乘法的思路计算二进制数的乘法体会
a <<= 1;
b >>>= 1;
}
return ans;
}
}