经典递归过程解析
预备内容
路径与递归
带路径的递归 vs 不带路径的递归(大部分 dp,状态压缩 dp 认为是路径简化了结构,dp 专题后续讲述)
任何递归都是 dfs 且非常灵活。回溯这个术语并不重要
传值方式
值传递:在递归中可以理解为值得副本拷贝,并不会改变值
引用传递:引用传递传递的是地址,指向的是同一份空间,会影响值
字符串的全部子序列
题目链接
https://www.nowcoder.com/practice/92e6247998294f2c933906fdedbc6e6a
思路分析
每个位置都分要和不要两种情况,子序列的总个数:2n
沿途收集路径,如果要回到上一个状态,需要恢复现场(回溯),再走下一个状态
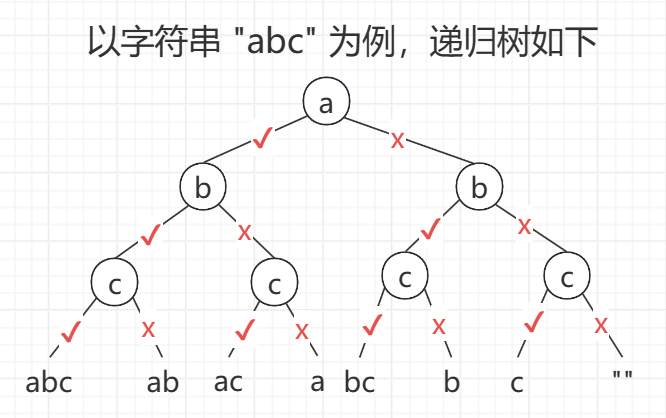
写法一
经典递归写法,递归沿途收集路径,如果需要回到上一个状态,恢复现场(回溯)
利用 HashSet 存储路径,同时实现去重
java
import java.util.*;
public class Solution {
// 题目是 String s,这里改成 str
public String[] generatePermutation(String str) {
char[] s = str.toCharArray();
HashSet<String> set = new HashSet<>();
// 将容器作为递归参数传递,可以复用空间
traversal(s, 0, new StringBuilder(), set);
String[] ans = new String[set.size()];
int i = 0;
for (String cur : set) {
ans[i++] = cur;
}
return ans;
}
public void traversal(char[] s, int i, StringBuilder path, HashSet<String> set) {
if (i == s.length) {
set.add(path.toString());
} else {
path.append(s[i]);
traversal(s, i + 1, path, set);
// 恢复现场
path.deleteCharAt(path.length() - 1);
traversal(s, i + 1, path, set);
}
}
}写法二
更优雅的实现,将数组作为递归参数传递,不断复用同一份空间,节省了空间开销
变量 i 表示当前遍历到的位置, size 表示 path 中填了多少个,即控制有效元素的个数
通过数组的复用和 i 变量,以及 size 控制有效元素的个数,在递归的过程中可以实现元素擦除,后面的元素会覆盖前面的元素,间接实现了恢复现场,无需手动控制
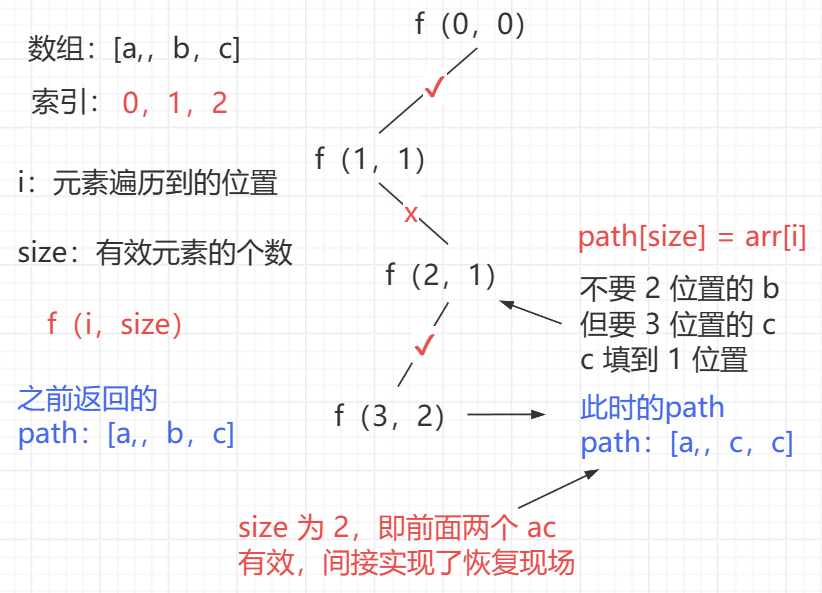
java
import java.util.*;
public class Solution {
// 题目是 String s,这里改成 str
public String[] generatePermutation(String str) {
char[] s = str.toCharArray();
HashSet<String> set = new HashSet<>();
// 将容器作为递归参数传递,可以复用空间
traversal(s, 0, new char[s.length], 0, set);
String[] ans = new String[set.size()];
int i = 0;
for (String cur : set) {
ans[i++] = cur;
}
return ans;
}
public void traversal(char[] s, int i, char[] path, int size, HashSet<String> set) {
if (i == s.length) {
set.add(String.valueOf(path, 0, size));
} else {
// 通过 size 控制来有效的元素
path[size] = s[i];
traversal(s, i + 1, path, size + 1, set);
traversal(s, i + 1, path, size, set);
}
}
}复杂度分析
时间复杂度:O(2n * n),子序列的个数:2n,每个子序列都要生成出来,平均长度算为 n
数组的全部组合(去重)
题目链接
https://leetcode.cn/problems/subsets-ii/
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的组合
答案不能包含重复的组合。返回的答案中,组合可以按 任意顺序排列
注意其实要求返回的不是子集,因为子集一定是不包含相同元素的,要返回的其实是不重复的组合,比如输入:nums = [1,2,2],输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
思路分析
如何区分不同的组合?组合中的每个数出现的个数不同,就是不同的组合
可以先对数组排序,这个操作并不会影响组合的个数

代码实现
java
class Solution {
public List<List<Integer>> subsetsWithDup(int[] nums) {
List<List<Integer>> ans = new ArrayList<>();
Arrays.sort(nums);
// 作为参数递归传递可以实现空间复用
traversal(nums, 0, new int[nums.length], 0, ans);
return ans;
}
public static void traversal(int[] nums, int i, int[] path, int size, List<List<Integer>> ans) {
if (i == nums.length) {
ArrayList<Integer> cur = new ArrayList<>();
for (int j = 0; j < size; j++) {
cur.add(path[j]);
}
ans.add(cur);
} else {
// 退出循环时,j 来到下一组的第一个数的位置
int j = i + 1;
while (j < nums.length && nums[i] == nums[j]) {
j++;
}
// 通过 size 控制要几个当前组的数
// 当前组的数要 0 个,从 j 位置开始继续递归求出组合
traversal(nums, j, path, size, ans);
// 当前组的数要 1 个,2 个,3 个... 每个情况都尝试一遍
for (; i < j; i++) {
path[size++] = nums[i];
traversal(nums, j, path, size, ans);
}
}
}
}复杂度分析
为什么分组可以达到剪枝的效果?对当前组每次选 0 个数,1 个数......
这个过程就是人为的控制当前组递归的过程,进而达到了剪枝的目的,而不是每遇到一个数都去展开,分情况讨论要和不要去求组合
例如:1 1 1 1 2 3 4 这个序列,前面有四个 1,若不剪枝,都要讨论要和不要的情况,相当于 24 的展开,而人为的控制分组,四个 1 这一组就只有五种情况,要 0 个 1,要 1 个 1......大大减少了不必要的递归,优化了时间
如果每一组的数出现多次,通过人为的分组控制递归的过程,是有利于优化实践复杂度的
最差的情况,每个数都出现了一次,那每个数都是选和不选两种情况,类似递归过程的二叉树那样展开
时间复杂度:O(2n * n),每个数都是选和不选两种情况,意思就是等价于求子序列的过程,子序列的个数:2n,每个子序列都要生成出来,平均长度算为 n
数组的全部排列
题目链接
https://leetcode.cn/problems/permutations
思路分析
区别于组合,组合是每个位置的数要和不要两种情况
对于排列,该位置之后包括当前位置的数字都要在当前位置都要出现一次,如下图解
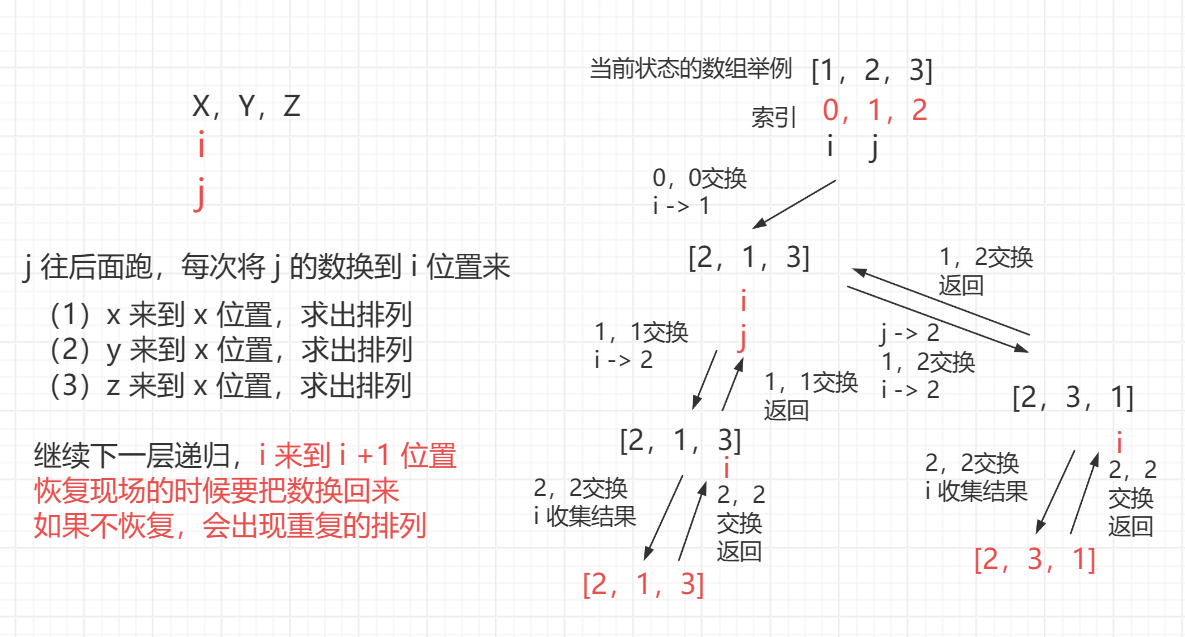
以上图解过程
java
for (int j = i; j < nums.length; j++) {
swap(nums, i, j);
traverse(nums, i + 1, ans);
swap(nums, i, j);
}代码实现
java
public class Solution {
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> ans = new ArrayList<>();
traverse(nums, 0, ans);
return ans;
}
public void traverse(int[] nums, int i, List<List<Integer>> ans) {
if (i == nums.length) {
List<Integer> cur = new ArrayList<>();
for (int num : nums) {
cur.add(num);
}
ans.add(cur);
} else {
for (int j = i; j < nums.length; j++) {
swap(nums, i, j);
traverse(nums, i + 1, ans);
swap(nums, i, j);
}
}
}
public void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}复杂度分析
时间复杂度:O(n! * n),排列的个数:n!,每个排列都要生成出来,平均长度算为 n
数组的全部排列(去重)
题目链接
https://leetcode.cn/problems/permutations-ii/
思路分析
思路和上体类似,需要保证每次换到 i 位置的数都是不同的,这里可以使用 HashSet 去重,递归前判断一下
代码实现
java
class Solution {
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> ans = new ArrayList<>();
traverse(nums, 0, ans);
return ans;
}
public void traverse(int[] nums, int i, List<List<Integer>> ans) {
if (i == nums.length) {
List<Integer> cur = new ArrayList<>();
for (int num : nums) {
cur.add(num);
}
ans.add(cur);
} else {
HashSet<Integer> hashSet = new HashSet<>();
for (int j = i; j < nums.length; j++) {
// 每次换到 i 位置的数都是不同的,实现去重
// 每遍历一个数就放到 set 中,后续判断是否出现过
// 如果当前遍历的数 set 中已经存在,说明是重复的数值
if (!hashSet.contains(nums[j])) {
hashSet.add(nums[j]);
swap(nums, i, j);
traverse(nums, i + 1, ans);
swap(nums, i, j);
}
}
}
}
public void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}递归函数逆序栈
思路分析
时间复杂度:O(n2)
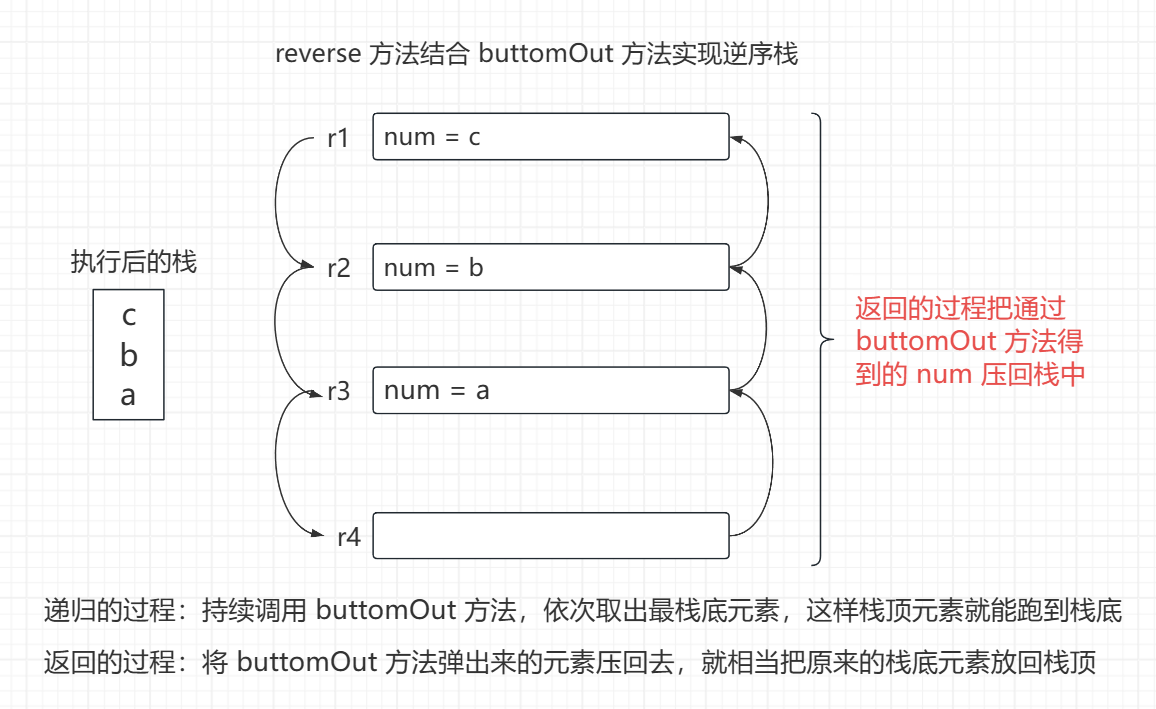
代码实现
java
import java.util.Stack;
public class Main {
public static void reverse(Stack<Integer> stack) {
if (stack.isEmpty()) {
return;
}
// 依次取出栈底元素,栈空了,要返回
// 返回的过程中将原来拿到的栈底元素压回去
// 相当于把栈底元素放到了栈顶,实现了逆序
int num = buttomOut(stack);
reverse(stack);
stack.push(num);
}
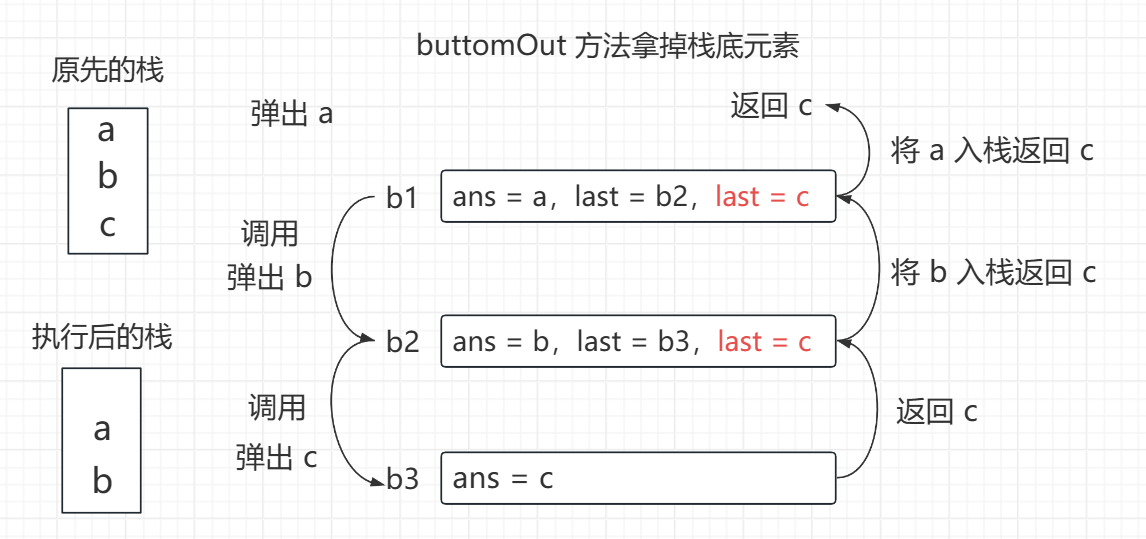
public static int buttomOut(Stack<Integer> stack) {
// 栈顶到栈底元素 a b c 为例
int ans = stack.pop();
if (stack.isEmpty()) {
// 拿完了 c,栈空,返回 c
return ans;
} else {
int last = buttomOut(stack);
// 把当时弹出的元素押回去
// 同时接收到返回的 c,一直向上返回
stack.push(ans);
return last;
}
}
public static void main(String[] args) {
Stack<Integer> stack = new Stack<Integer>();
stack.push(1);
stack.push(2);
stack.push(3);
stack.push(4);
stack.push(5);
// 原先从栈顶到栈底 5 4 3 2 1
// 逆序后从栈顶到栈底 1 2 3 4 5
// 依次弹出栈顶元素 1 2 3 4 5
reverse(stack);
while (!stack.isEmpty()) {
System.out.println(stack.pop());
}
}
}递归函数排序栈
题目要求
请完成无序栈的排序,要求排完序之后,从栈顶到栈底从小到大
只能使用栈提供的 push、pop、isEmpty 三个方法、以及递归函数
除此之外不能使用任何的容器,数组也不行
思路分析
时间复杂度:O(n2)
首先统计栈的深度,记为 deep,统计最大值出现的次数,记为 k
然后在 deep 层这个范围内找到最大值,将所有最大值沉底
由于最大值沉底了,这部分排好序了,下一轮可以不用管
下一轮在 deep - k 层这个范围内找最大值,沉底,如此往复,从栈底到栈顶就是逐渐减小的,即从栈顶到栈底是从小到大排列的,这样就可以实现排序
代码实现
java
import java.util.Stack;
public class Main {
public static void sort(Stack<Integer> stack) {
int deep = deep(stack);
while (deep > 0) {
// 找到最大值
int max = max(stack, deep);
// 最大值出现的次数
int k = times(stack, deep, max);
// 将所有最大值沉底
down(stack, deep, max, k);
// 最大值占用了 k 层
// 下一轮在 deep - k 层继续找最大,沉底
// 依次往复,这样就可以实现栈排序
deep -= k;
}
}
public static int deep(Stack<Integer> stack) {
if (stack.isEmpty()) {
return 0;
}
int num = stack.pop();
int deep = deep(stack) + 1;
stack.push(num);
return deep;
}
// 从栈当前的顶部开始,往下数 deep 层
// 返回这 deep 层里的最大值
public static int max(Stack<Integer> stack, int deep) {
if (deep == 0) {
return Integer.MIN_VALUE;
}
int num = stack.pop();
int restMax = max(stack, deep - 1);
int max = Math.max(num, restMax);
stack.push(num);
return max;
}
// 从栈当前的顶部开始,往下数 deep 层,已知最大值 max
// 返回 max 出现了几次,不改变栈中元素的相对次序
public static int times(Stack<Integer> stack, int deep, int max) {
if (deep == 0) {
return 0;
}
int num = stack.pop();
int restTimes = times(stack, deep - 1, max);
// 总出现次数 = 底下层的出现次数 + 当前层出现次数
int times = restTimes + (num == max ? 1 : 0);
stack.push(num);
return times;
}
// 从栈当前的顶部开始往下数 deep 层,已知最大值 max,出现了 k 次
// 请把这 k 个最大值沉底,剩下的数保持相对次序不变放回栈中
public static void down(Stack<Integer> stack, int deep, int max, int k) {
if (deep == 0) {
// 递归到最底层,把 max 压入
// 返回的时候把原来的元素压回去
// 实现了将最大元素沉底的操作
for (int i = 0; i < k; i++) {
stack.push(max);
}
} else {
int num = stack.pop();
down(stack, deep - 1, max, k);
// 递归前取出来了,返回的时候压回去
// 由于递归是一层一层往下,返回是从下往上返回
// 类似栈的结构,后面取出的元素先压回,可以维持相对次序
if (num != max) {
stack.push(num);
}
}
}
// 为了测试
// 生成随机栈
public static Stack<Integer> randomStack(int n, int v) {
Stack<Integer> ans = new Stack<Integer>();
for (int i = 0; i < n; i++) {
ans.add((int) (Math.random() * v));
}
return ans;
}
// 为了测试
// 检测栈是不是从顶到底依次有序
public static boolean isSorted(Stack<Integer> stack) {
int step = Integer.MIN_VALUE;
while (!stack.isEmpty()) {
if (step > stack.peek()) {
return false;
}
step = stack.pop();
}
return true;
}
// 为了测试
public static void main(String[] args) {
Stack<Integer> test = new Stack<Integer>();
test.add(1);
test.add(5);
test.add(4);
test.add(5);
test.add(3);
test.add(2);
test.add(3);
test.add(1);
test.add(4);
test.add(2);
sort(test);
while (!test.isEmpty()) {
System.out.println(test.pop());
}
// 随机测试
int N = 20;
int V = 20;
int testTimes = 20000;
System.out.println("测试开始");
for (int i = 0; i < testTimes; i++) {
int n = (int) (Math.random() * N);
Stack<Integer> stack = randomStack(n, V);
sort(stack);
if (!isSorted(stack)) {
System.out.println("出错了!");
break;
}
}
System.out.println("测试结束");
}
}汉诺塔问题
问题背景
三根柱子 A、B、C,柱子上有大小不同的圆盘,初始时所有圆盘在 A 柱子上
需要将所欲圆盘从 A 柱子移动到 C 柱子,且移动过程中必须满足大圆盘在小圆盘的下面
给定圆盘 n,打印将所有圆盘从 A 柱子移动到 C 柱子的移动过程
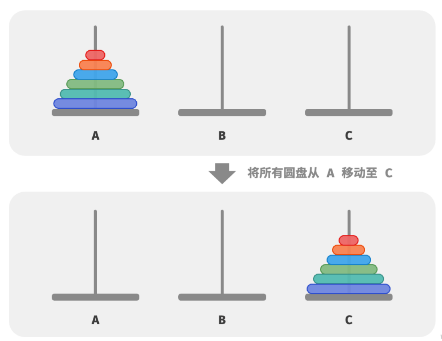
思路分析
递归思想:一个问题可以拆分成一个简单的问题和一个复杂问题
设置 from,为起始柱,to 为目标柱,other 为中间柱三个参数
将上面的 n - 1 个圆盘看做整体,视为一个复杂的问题,最底层的圆盘看作一个简单的问题
移动思路:将上面的 n - 1 个圆盘从 from 柱移动到 other 柱,将最底层的圆盘从 from 柱移动到 to 柱,将 n - 1 个圆盘从 other 柱移动到 to 柱(可以类比两个圆盘的情况理解)
而上面的 n -1 个圆盘这个复杂的问题,如何从 from 柱移动到 other 柱子呢,又可以复用递归的思想
将上面的 n - 2 个圆盘从 from 柱移动到 other 柱,将第 n - 1 个圆盘从 from 柱移动到 to 柱,将 n - 2 个圆盘从 other 柱移动到 to 柱......
代码实现
java
// 打印n层汉诺塔问题的最优移动轨迹
public class Code07_TowerOfHanoi {
public static void hanoi(int n) {
if (n > 0) {
f(n, "左", "右", "中");
}
}
public static void f(int i, String from, String to, String other) {
// 只有一个圆盘
if (i == 1) {
System.out.println("移动圆盘 1 从 " + from + " 到 " + to);
} else {
// from 左边的柱子,other 中间的柱子,to 右边的柱子
f(i - 1, from, other, to);
System.out.println("移动圆盘 " + i + " 从 " + from + " 到 " + to);
f(i - 1, other, to, from);
}
}
public static void main(String[] args) {
int n = 3;
hanoi(n);
}
}移动次数
给定 n 个圆盘,将所有圆盘从 A 柱子移动到 C 柱子所需要的移动次数:2 n - 1
将上面的 n - 1 个圆盘从 from 柱子移动到 other 柱子:f(n - 1)
将最底层的圆盘从 from 柱子移动到 to 柱子:1
将 n - 1 个圆盘从 other 柱子移动到 to 柱子:f(n - 1)
总过程:f(n) = f(n - 1) + 1 + f(n - 1) = 2 * f(n - 1) + 1
根据数学递推关系可以得到通项公式为 2 n - 1
