N皇后问题(位运算)
问题背景
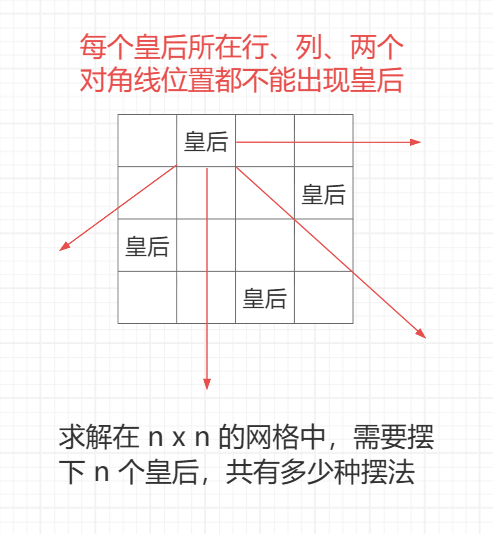
统计方案数
题目链接
https://leetcode.cn/problems/n-queens-ii/description/
思路分析
(1)递归实现
在第一行的第 1 个位置放置皇后,以此为基础,之后在第 2 - n-1 行中的每一列都尝试一遍,看摆放皇后是否合法
在第一行的第 2 个位置放置皇后,以此为基础,之后在第 2 - n-1 行中的每一列都尝试一遍,看摆放皇后是否合法
.....
直到第一行每一个位置都尝试了的情况下,下面所有行的所有列都尝试过了,整个过程结束
(2)位运算实现
int 类型有 32 位,用每一个二进制位的状态来表示是否可以摆放皇后
某一列放置了皇后,则该列对应的二进制位为 1,否则为 0
col 表示列限制,left 表示右上到左下对角线的限制,right 表示左上到右下对角线的限制,具体是如何限制的可以看代码注释解析
这三个变量的二进制位,都用 1 表示不可以放置皇后,0 表示可以放置皇后,那共同的限制就是三个数做或运算得到的结果
int col : 0..i-1 行皇后放置的位置因为正下方向延伸的原因,哪些列不能再放皇后
int left : 0..i-1 行皇后放置的位置因为左下方向延伸的原因,哪些列不能再放皇后
int right : 0..i-1 行皇后放置的位置因为右下方向延伸的原因,哪些列不能再放皇后
根据 col、left、right,用位运算快速判断能放哪些列
把能放的列都尝试一遍,每次尝试修改 3 个数字表示当前的决策,后续返回的答案都累加返回
更多的思路和细节见代码注释......
check 函数
每行放置一个皇后,到后面的行尝试所有情况,即逐行尝试每一列是否可以放置皇后,此时无需考虑皇后所在行是否合法的情况
检查皇后两个对角线的位置可以使用斜率,这是很巧妙的地方,如果斜率的绝对值相等,则表示 45 度 135 度两个方向的对角线
新增 path 数组,表示第 i 行的皇后放置在了第 j 列,即 path[i] = j
检查皇后所在列可以检查 path 数组,遍历每一行,如果当前行皇后所在列和之前的皇后所在列相等,则表示在同一列,不合法
递归实现
java
class Solution {
// 用数组表示路径实现的 N 皇后问题,不推荐
public int totalNQueens(int n) {
if (n < 1) {
return 0;
}
return traversal(0, new int[n], n);
}
// i :当前来到的行
// path : 记录 0 ... i-1 行的皇后都摆在了那些列
// n :几皇后问题
// 0 ... i-1 行已经摆好了,返回 i ... n-1 行可以尝试的情况下还能找到几种有序的方法
public int traversal(int i, int[] path, int n) {
// 摆皇后是有前提的,如果可以递归到最后
// 说明所有的皇后都可以摆放,这时就是一种方法,返回
if (i == n) {
return 1;
}
int ans = 0;
// 当前来到第 i 行,尝试该行的每一个位置,即第 i 行的每一列
// n * n 的网格,即 n 行 n 列
for (int j = 0; j < n; j++) {
if (check(path, i, j)) {
// 皇后摆在第 i 行的第 j 列
path[i] = j;
ans += traversal(i + 1, path, n);
}
}
return ans;
}
// 检查 (i,j) 位置是否可以摆放皇后,第 i 行,第 j 列
public boolean check(int[] path, int i, int j) {
// 只需要检查该皇后列和对角线,皇后所在行无需检查
// 因为递归思路是每行摆一个皇后,到下一行开始尝试
// 不同的情况,不存在同一行出现两个皇后的情况
// 遍历皇后所在的列,坐标中也就是行的变化,遍历行
for (int k = 0; k < i; k++) {
// k :0 ... k-1
// 之前的行 : k
// 之前的列 : path[k]
// 在同一列或者对角线上就是不合法的
// 对角线可以用斜率来判断,这是巧妙的地方
if (j == path[k] || Math.abs(i - k) == Math.abs(j - path[k])) {
return false;
}
}
return true;
}
}位运算实现
java
class Solution {
// 位运算版本,常数时间极好,但是复杂度无法改变,仍是 O(n!)
public int totalNQueens(int n) {
if (n < 1) {
return 0;
}
// n = 5
// 1 << 5 = 0...100000 - 1
// limit = 0...011111
// limit 表示几皇后,即皇后的规模
int limit = (1 << n) - 1;
return traversal(limit, 0, 0, 0);
}
// limit 表示几皇后问题,col 列限制
// left 右上到左下的对角线限制
// right 左上到右下的对角线限制
public int traversal(int limit, int col, int left, int right) {
// 如果相等说明每一列都摆了皇后,而摆皇后是有前提的
// 能摆说明这些皇后是合法的,即这是一种摆放情况,返回
if (col == limit) {
return 1;
}
// 三者都用二进制位 0 表示可以放皇后,1 不可以放皇后
// 三者做或运算的结果表示 --> 总限制
int ban = col | left | right;
// 对 ban 取反,即 1 表示可以放皇后,0 不可以放皇后
// limit 表示几皇后问题,且对应的二进制位都是 1
// 然而更高的二进制位是无效的,& 运算后高位的二进制为
// 变为 0,则表示不能放置皇后,即 & 的目的就是取出那些
// 有效的二进制位,这些二进制位为 1 的表示可以尝试放皇后
// 即 candidate 表示可以哪些位置可以放置皇后
int candidate = limit & (~ban);
// 放置皇后的尝试
int place = 0;
// 一共有多少有效的方法
int ans = 0;
// 如果 candidate != 0 说明二进制位还有 1,可以放置皇后,继续尝试
while (candidate != 0) {
// Brian Kernighan 算法,提取出最右侧的 1 这个状态
// 例如 0 0 0 1 1 0 --> 0 0 0 0 1 0
// candidate : 0 0 1 1 1 0
// index : 5 4 3 2 1 0
// 3 2 1 位置表示可以放置皇后
// 那就每次提取出最右侧的 1
// 而 1 表示可以放置皇后
// 即 place 表示每一个可以尝试的位置
place = candidate & (-candidate);
// 二进制 0 0 1 1 1 0
// 下标 5 4 3 2 1 0
// 提取出最右侧的 1
// place :
// 0 0 0 0 1 0
// candidate :
// 0 0 1 1 0 0
// 5 4 3 2 1 0
// 尝试过了,该位要变成 0,表示不能放置皇后
// 异或运算实现,异或运算:不同为 0,相同为 1
candidate ^= place;
// 哪些位的二进制位为 1,表示该二进制位对应的限制在这个
// 二进制位的位置上不可以放置皇后,否则为 0 表示可以放置
// col 列限制,如果某个位置为 1,表示该位置放置了皇后
// 则该位置对应的列不可以放置皇后,这样达到限制的目的
// place 表示可以尝试的位置,该位置要尝试,使用或运算实现将该二进制位置为 1
// 两个注意点
// (1)每次尝试都会走到下一行
// (2)即若某个位置需要放置皇后,使用或运算将该二进制为置为 1 即可
// left 表示从右上到左下的限制,left | place 表示原有的限制下,某个位置需要放置皇后
// 整体的运算结果右移就表示放置新的皇后之后,新的限制
// 如何理解?整体右移在列的体现上是走向低位的体现,然后右上到左下不正是左下方走向低位
// 限制的这个趋势,对应上了
// right 和 left 同理,这里不再赘述,过程是相反的
// 上面的 candidate ^= place 表示本行已经尝试过了,现在需要到下一行继续尝试
// 所以调用递归,同时把该位置尝试后新的限制传递给下一层
ans += traversal(limit, col | place, (left | place) >> 1, (right | place) << 1);
}
return ans;
}
}输出放置方案
题目链接
https://leetcode.cn/problems/n-queens/description/
思路分析
该题通过 path 数组记录了每一行的皇后放置在什么位置,遍历整个棋盘,做判断即可
递归实现
java
import java.util.*;
class Solution {
// 用数组表示路径实现的 N 皇后问题,不推荐
public List<List<String>> solveNQueens(int n) {
if (n < 1) {
return new ArrayList<>();
}
List<List<String>> result = new ArrayList<>();
int[] path = new int[n]; // path[i] 表示第 i 行的皇后在第几列
traversal(0, path, n, result);
return result;
}
// i :当前来到的行
// path : 记录 0 ... i-1 行的皇后都摆在了那些列
// n :几皇后问题
// result:用于收集所有解
public void traversal(int i, int[] path, int n, List<List<String>> result) {
// 摆皇后是有前提的,如果可以递归到最后
// 说明所有的皇后都可以摆放,这时就是一种方法,构造解并加入结果
if (i == n) {
// 构建棋盘,记录此时的摆放情况
List<String> board = new ArrayList<>();
// 遍历每一行每一列,逐行加入 borad 中
for (int row = 0; row < n; row++) {
StringBuilder sb = new StringBuilder();
for (int col = 0; col < n; col++) {
// 对于每一行的每一列判断,是否放置了皇后
// path[row] 表示 row 行的 path[row] 列放置了皇后
if (col == path[row]) {
sb.append('Q');
} else {
sb.append('.');
}
}
board.add(sb.toString());
}
result.add(board);
return;
}
// 当前来到第 i 行,尝试该行的每一个位置,即第 i 行的每一列
for (int j = 0; j < n; j++) {
if (check(path, i, j)) {
// 皇后摆在第 i 行的第 j 列
path[i] = j;
traversal(i + 1, path, n, result);
}
}
}
// 检查 (i,j) 位置是否可以摆放皇后,第 i 行,第 j 列
public boolean check(int[] path, int i, int j) {
// 只需要检查该皇后列和对角线,皇后所在行无需检查
// 因为递归思路是每行摆一个皇后,到下一行开始尝试
// 不同的情况,不存在同一行出现两个皇后的情况
// 遍历皇后所在的列,坐标中也就是行的变化,遍历行
for (int k = 0; k < i; k++) {
// k :0 ... k-1
// 之前的行 : k
// 之前的列 : path[k]
// 在同一列或者对角线上就是不合法的
// 对角线可以用斜率来判断,这是巧妙的地方
if (j == path[k] || Math.abs(i - k) == Math.abs(j - path[k])) {
return false;
}
}
return true;
}
}时间对比测试
问题分析
位运算实现的版本常数时间极好,大量优化了额常数时间,同时省去了很多数组寻址的过程
<= 16 皇后问题,位运算版本在 10 s 内可以跑完,而递归版本要跑很久
> 16 皇后问题,无论哪个版本都会跑很久,因为是 n!的增长
代码实现
java
// N皇后问题
// 测试链接 : https://leetcode.cn/problems/n-queens-ii/
public class Test {
// 用数组表示路径实现的N皇后问题,不推荐
public static int totalNQueens1(int n) {
if (n < 1) {
return 0;
}
return f1(0, new int[n], n);
}
// i : 当前来到的行
// path : 0...i-1行的皇后,都摆在了哪些列
// n : 是几皇后问题
// 返回 : 0...i-1行已经摆完了,i....n-1行可以去尝试的情况下还能找到几种有效的方法
public static int f1(int i, int[] path, int n) {
if (i == n) {
return 1;
}
int ans = 0;
// 0 1 2 3 .. n-1
// i j
for (int j = 0; j < n; j++) {
if (check(path, i, j)) {
path[i] = j;
ans += f1(i + 1, path, n);
}
}
return ans;
}
// 当前在i行、j列的位置,摆了一个皇后
// 0...i-1行的皇后状况,path[0...i-1]
// 返回会不会冲突,不会冲突,有效!true
// 会冲突,无效,返回false
public static boolean check(int[] path, int i, int j) {
// 当前 i
// 当列 j
for (int k = 0; k < i; k++) {
// 0...i-1
// 之前行 : k
// 之前列 : path[k]
if (j == path[k] || Math.abs(i - k) == Math.abs(j - path[k])) {
return false;
}
}
return true;
}
// 用位信息表示路径实现的N皇后问题,推荐
public static int totalNQueens2(int n) {
if (n < 1) {
return 0;
}
// n = 5
// 1 << 5 = 0...100000 - 1
// limit = 0...011111;
// n = 7
// limit = 0...01111111;
int limit = (1 << n) - 1;
return f2(limit, 0, 0, 0);
}
// limit : 当前是几皇后问题
// 之前皇后的列影响:col
// 之前皇后的右上 -> 左下对角线影响:left
// 之前皇后的左上 -> 右下对角线影响:right
public static int f2(int limit, int col, int left, int right) {
if (col == limit) {
// 所有皇后放完了!
return 1;
}
// 总限制
int ban = col | left | right;
// ~ban : 1可放皇后,0不能放
int candidate = limit & (~ban);
// 放置皇后的尝试!
int place = 0;
// 一共有多少有效的方法
int ans = 0;
while (candidate != 0) {
// 提取出最右侧的1
// 0 0 1 1 1 0
// 5 4 3 2 1 0
// place :
// 0 0 0 0 1 0
// candidate :
// 0 0 1 1 0 0
// 5 4 3 2 1 0
// place :
// 0 0 0 1 0 0
// candidate :
// 0 0 1 0 0 0
// 5 4 3 2 1 0
// place :
// 0 0 1 0 0 0
// candidate :
// 0 0 0 0 0 0
// 5 4 3 2 1 0
place = candidate & (-candidate);
candidate ^= place;
ans += f2(limit, col | place, (left | place) >> 1, (right | place) << 1);
}
return ans;
}
public static void main(String[] args) {
int n = 14;
long start, end;
System.out.println("测试开始");
System.out.println("解决" + n + "皇后问题");
start = System.currentTimeMillis();
System.out.println("方法1答案 : " + totalNQueens1(n));
end = System.currentTimeMillis();
System.out.println("方法1运行时间 : " + (end - start) + " 毫秒");
start = System.currentTimeMillis();
System.out.println("方法2答案 : " + totalNQueens2(n));
end = System.currentTimeMillis();
System.out.println("方法2运行时间 : " + (end - start) + " 毫秒");
System.out.println("测试结束");
System.out.println("=======");
System.out.println("只有位运算的版本,才能10秒内跑完16皇后问题的求解过程");
start = System.currentTimeMillis();
int ans = totalNQueens2(16);
end = System.currentTimeMillis();
System.out.println("16皇后问题的答案 : " + ans);
System.out.println("运行时间 : " + (end - start) + " 毫秒");
}
}复杂度分析
时间复杂度:O(n!)
每次是逐行放置皇后,所以不考虑皇后所在行的影响
第一行有 n 种尝试,忽略对角线的影响,只看同一列不能出现皇后,第二行有 n - 1 中尝试,依次类推,而所有的可能属于是相乘的关系
n * (n - 1) * (n - 2) * ... * 1 = n!
更大的皇后问题?
目前能算出精确解数的 n 皇后问题,最大 n 为 27,其解数约为 234907967154122528
这个结果是依靠分布式计算集群 + 极致的位运算剪枝回溯算法,耗费大量时间得到的
对于 n=28 及以上的情况,哪怕是用超级计算机,也无法在可接受的时间内完成穷举计算
核心瓶颈在于
(1)时间复杂度接近 n!,n 每增加 1,计算量会呈阶乘级暴涨
(2)并行计算的节点通信开销、状态存储开销会随 n 增大急剧上升
