构建前缀信息的技巧
⭐ 常用技巧
构建某个前缀信息最早出现、最晚出现、出现次数等,是很常见的技巧,除此之外,还有很多种类的前缀信息可以构建出来,解决很多子数组相关问题
一维前缀和
题目链接
https://leetcode.cn/problems/range-sum-query-immutable/
思路分析
构建前缀和数组

代码实现
java
class NumArray {
public int[] sum;
public NumArray(int[] nums) {
sum = new int[nums.length + 1];
// 0 位置不用,从 1 开始统计前缀和
// 此时的 i 表示物理位置,即第几个数
// 所以在 nums 数组中 i 位置的数的下标索引为 i - 1
for (int i = 1; i <= nums.length; i++) {
// 当前位置的前缀和 = 前一个数的前缀和 + 当前数字
sum[i] = sum[i - 1] + nums[i - 1];
}
}
public int sumRange(int left, int right) {
// [left, right] ,对应第 left + 1 个数到第 right + 1 个数
// 前缀和为第 right + 1 个数的前缀和 - 第 left 个数的前缀和
return sum[right + 1] - sum[left];
}
}
/**
* Your NumArray object will be instantiated and called as such:
* NumArray obj = new NumArray(nums);
* int param_1 = obj.sumRange(left,right);
*/和为 aim 的最长子数组
题目链接
https://www.nowcoder.com/practice/36fb0fd3c656480c92b569258a1223d5
思路分析
构建前缀和最早出现的位置
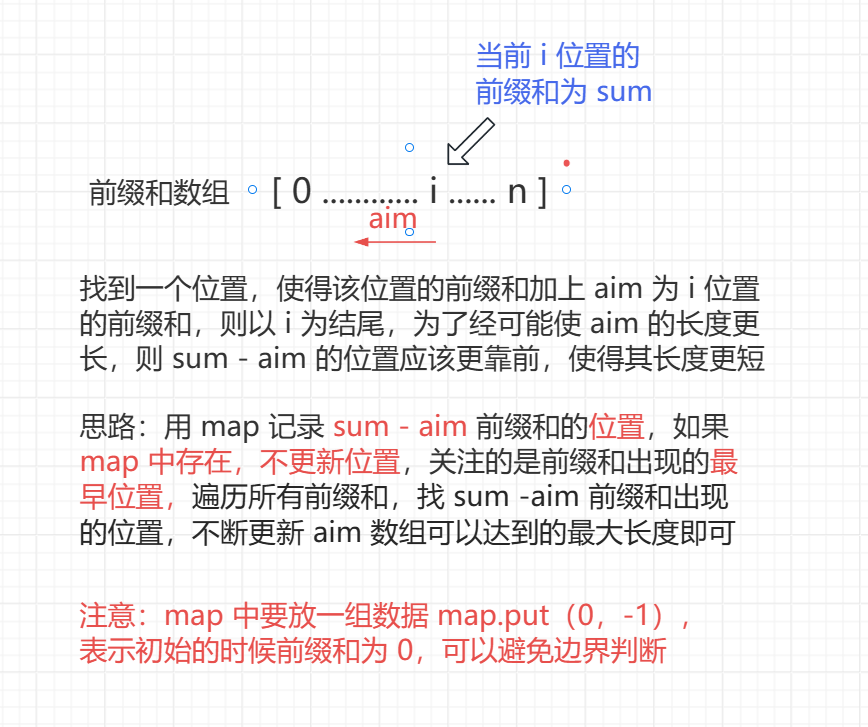
Tip
例如:aim 为 5,而数组只有 5,下标为 0
(1)0 位置的前缀和 sum = 5
(2)查询 sum - aim = 0 这个前缀和出现在哪,发现没有出现过
(3)但是 5 自己可以构成一个子数组,使得子数组的和为 aim,错过答案了
为什么会错失答案?原因是 0 -1 这条记录没加,因为 0 这个前缀和在没有数的时候就出现了
代码实现
java
import java.io.*;
import java.util.HashMap;
public class Main {
public static int MAXN = 100001;
public static int[] arr = new int[MAXN];
public static int n, aim;
// key : 某个前缀和
// value : 这个前缀和最早出现的位置
public static HashMap<Integer, Integer> map = new HashMap<>();
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken() != StreamTokenizer.TT_EOF) {
n = (int) in.nval;
in.nextToken();
aim = (int) in.nval;
for (int i = 0; i < n; i++) {
in.nextToken();
arr[i] = (int) in.nval;
}
out.println(compute());
}
out.flush();
out.close();
br.close();
}
public static int compute() {
map.clear();
// 重要的地方,需要放入 0 -1 这组数据
// 0 这个前缀和,一个数字也没有的时候久存在了
map.put(0, -1);
int ans = 0;
for (int i = 0, sum = 0; i < n; i++) {
sum += arr[i];
// 如果前缀和出现过,不更新,只记录最早出现的位置
if (map.containsKey(sum - aim)) {
ans = Math.max(ans, i - map.get(sum - aim));
}
if (!map.containsKey(sum)) {
map.put(sum, i);
}
}
return ans;
}
}和为 aim 的子数组个数
题目链接
https://leetcode.cn/problems/subarray-sum-equals-k/
思路分析
构建前缀和的出现的次数
本题是上一题的转化,统计 sum - aim 前缀和出现的次数即为和为 K 的子数组个数
⚠️ 注意:将 0 1 这组数据放入 map 中,表示 0 这个前缀和在没有数字的时候已经出现了 1 次
代码实现
java
class Solution {
// 原来是 int k,这里改成 aim
public int subarraySum(int[] nums, int aim) {
HashMap<Integer, Integer> map = new HashMap<>();
// 表示没有数字的时候, 0 这个前缀和就已经出现了 1 次
map.put(0, 1);
int ans = 0;
for (int i = 0, sum = 0; i < nums.length; i++) {
sum += nums[i];
// sum - aim 这个前缀和出现的次数即为 ans
ans += map.getOrDefault(sum - aim, 0);
// 记得统计 sum 前缀和出现次数
map.put(sum, map.getOrDefault(sum, 0) + 1);
}
return ans;
}
}元素个数相同的最长子数组
题目链接
https://www.nowcoder.com/practice/545544c060804eceaed0bb84fcd992fb
思路分析
构建前缀和最早出现的位置
对于元素个数相同的问题,可以转化为状态,例如:正数认为是 1,负数认为是 -1
因为元素个数相同,即转化为求累加和 aim = 0 的最长子数组长度,转化为第一题
⚠️ 注意:将 0 -1 这组数据放入 map 中,表示 0 这个前缀和在没有数字的时候已经出现了
代码实现
java
import java.io.*;
import java.util.HashMap;
public class Main {
public static int MAXN = 100001;
public static int[] arr = new int[MAXN];
public static int n;
public static HashMap<Integer, Integer> map = new HashMap<>();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken() != StreamTokenizer.TT_EOF) {
n = (int) in.nval;
for (int i = 0, num; i < n; i++) {
in.nextToken();
num = (int) in.nval;
// 状态转化,正数认为是 1,负数认为是 -1
arr[i] = num != 0 ? (num > 0 ? 1 : -1) : 0;
}
out.println(compute());
}
out.flush();
out.close();
br.close();
}
public static int compute() {
map.clear();
map.put(0, -1);
int ans = 0;
for (int i = 0, sum = 0; i < n; i++) {
sum += arr[i];
if (map.containsKey(sum)) {
ans = Math.max(ans, i - map.get(sum));
} else {
map.put(sum, i);
}
}
return ans;
}
}表现良好的最长时间段
题目链接
https://leetcode.cn/problems/longest-well-performing-interval/
思路分析
构建前缀和最早出现的位置
题意中有效子数组指的是 (> 8 的元素个数) > (<= 8 的元素个数),需要找出最长的
还是可以做状态转化,将 > 8 认为是 1,<= 8 认为是 -1,即求子数组累加和 >= 1 的最长子数组
情况一:i 位置的前缀和 > 0,说明(> 8 的元素个数) > (<= 8 的元素个数) 这个条件成立,则最长子数组的长度为 i + 1
情况二:i 位置的前缀和 < 0,而数组转化后不是 1 就是 -1,如果前缀和要增加或者减少,那也只能一点点的增加或者减少,例如 i 位置的前缀和为 -3,只需要找前缀和为 -4 的最早出现在哪里,例如说有一个前缀和为 -5,则它的位置一定在 -4 的后边,又比如有一个前缀和为 -6,则它的位置一定在 -5 的后边,因为数组中只有 1 和 -1,前缀和只能一点点的增加或者减少,即只有查找前缀和 -4 出现的最早位置才能使得有效数组的长度尽可能的长
⚠️ 注意:将 0 -1 这组数据放入 map 中,表示 0 这个前缀和在没有数字的时候已经出现了
代码实现
java
class Solution {
public int longestWPI(int[] hours) {
HashMap<Integer, Integer> map = new HashMap<>();
// 0 这个前缀和在一个数也没有的时候就已经出现了
map.put(0, -1);
int ans = 0;
for (int i = 0, sum = 0; i < hours.length; i++) {
// 状态转化
sum += hours[i] > 8 ? 1 : -1;
// 此时的子数组符合题目要求
if (sum > 0) {
ans = i + 1;
} else {
// sum < 0,找前缀和 sum - 1 的最早出现位置
if (map.containsKey(sum - 1)) {
ans = Math.max(ans, i - map.get(sum - 1));
}
}
if (!map.containsKey(sum)) {
map.put(sum, i);
}
}
return ans;
}
}使数组和能被 P 整除
题目链接
https://leetcode.cn/problems/make-sum-divisible-by-p/description/
思路分析
构建前缀和余数最晚出现的位置
设置一个 map,key 为前缀和 % p 的余数,value 为最晚出现位置
假设一个数组整体和 % p 的余数为 4,0 到 i 位置的和 % p 的余数为 6,从 i 位置往前面找,拿掉一个子数组和 % p 的余数为 4 的,就可以实现整个数组可以被 p 整除
那如何找到余数为 4 的这个子数组,且使其尽量的短呢?即只需要寻找余数为 2 (6 - 4)的子数组的最晚出现位置,遍历每一个位置的 i,不断更新最短子数组的长度即可
情况一:i 位置的余数 cur > 整体的余数 mod,需要找余数 i - cur 的最晚出现位置
情况二:i 位置的余数 cur < 整体的余数 mod,需要找余数 cur - mod + p 的最晚出现位置
为什么要 +p ?因为题目中的数据给定 num [ i ] >= 1,即余数不会出现负数, +p 可以等效处理,具体原因见同余定理笔记中减法同余的 Tip 部分内容,做了详细的解释
⚠️ 注意:将 0 -1 这组数据放入 map 中,表示 0 这个前缀和在没有数字的时候已经出现了
代码实现
java
class Solution {
public int minSubarray(int[] nums, int p) {
// 整体余数
int mod = 0;
// 性质的逆运用:(a % p) % p 等价于 a % p
// 带入逐步递归,最后发现就是对整体求和然后 % p
for (int num : nums) {
mod = (mod + num) % p;
}
if (mod == 0) {
return 0;
}
// key :前缀和 %p 的余数
// value :最晚出现的位置
HashMap<Integer, Integer> map = new HashMap<>();
// 0 这个前缀和在一个数也没有的时候就出现了
map.put(0, -1);
int ans = Integer.MAX_VALUE;
for (int i = 0, cur = 0, find; i < nums.length; i++) {
// 0 ... i 这部分的余数
cur = (cur + nums[i]) % p;
find = cur >= mod ? (cur - mod) : (cur + p - mod);
// find = (cur + p - mod) % p;
if (map.containsKey(find)) {
ans = Math.min(ans, i - map.get(find));
}
// 因为要的是最晚位置,直接更新
map.put(cur, i);
}
return ans == nums.length ? -1 : ans;
}
}⭐ 区间和取模的写法
加法同余性质:(a + b) % p = (a % p + b % p) % p,即 a % p 等价于 (a % p) % p
第一轮推导:mod = (0 + x1) % p = (x1)% p
第二轮推导:mod = ((x1 % p) + x2) % p = (x1 + x2) % p,标红部分是性质的逆应用
.................
第 n 轮推导: mod = ((X1 % p) + ... + (Xn-1 % p) + Xn) % p = (x1 + ... + xn) % p
对于 0 到 i 这个区间,该区间的和 %p 的结果为,for 循环遍历每个数,初始 mod = 0
mod = (mod + num [ i ])% p
java
// 1. 求整个数组的和 %p 的结果
int mod = 0;
for (int num : nums) {
mod = (mod + num) % p;
}
// 2. 给定区间 0,i,求该区间和 %p 的结果
long mod = 0; // 防止溢出,更安全的写法
for (int i = 0; i < nums.length; i++) {
mod = (mod + nums[i]) % p;
// 余数小于 0,而余数要求取正数,+p
// 为什么 +p 可以用减法同余来理解
if (mod < 0) {
mod += p;
}
// 取余前缀和,表示 i 位置即之前所有数之和取余的结果
// 注意:sum 数组基于一位前缀和模板,采用 n + 1 的长度,0 位置不用
sum[i + 1] = (int) mod;
}
// 3. 给定区间 i,j,求该区间所有数求和取余的结果
// 考虑到余数可能为负数,+p 处理
// 注意:sum 数组基于一位前缀和模板,采用 n + 1 的长度,0 位置不用
int ans = (sum[j + 1] - sum[i] + p) % p;偶数次元音的最长子字符串
题目链接
https://leetcode.cn/problems/find-the-longest-substring-containing-vowels-in-even-counts/
思路分析
构建前缀奇偶状态最早出现的位置
对于 a e i o u 这五位,出现偶数次,记为状态 0,出现奇数次,记为状态 1,可以用位运算表示
对于一个字串,0 到 i 位置 a e i o u 有一个状态,那只需要在 i 位置往前寻找一个前缀字符串,该字符串的状态和 0 到 i 的状态相同,那中间的字串的每个字符就是出现偶数次的,为什么?
对于每一个字符,奇数 + 偶数 = 奇数,偶数 + 偶数 = 偶数,利用奇偶性来推测
代码实现
java
class Solution {
public int findTheLongestSubstring(String s) {
int n = s.length();
// 偶数次,记为状态 0,出现奇数次,记为状态 1
// 只有 5 个元音字符,状态就是 5 位,32 位就够用了
// map[i] 表示状态 i 对应的最长子串的长度
int[] map = new int[32];
// 例如 map[...01100] = -2
// 用 -2 表示这个状态之前没有出现过
Arrays.fill(map, -2);
// 0 0 0 0 0
// u o i e a
// 上面这个状态天然是偶数状态,用 -1 表示
// 在一个数也没有的时候就出现过了
map[0] = -1;
int ans = 0;
for (int i = 0, status = 0, m; i < n; i++) {
// status 表示 0 ... i-1 字符串上 a e i o u 的奇偶性
// s[i] 表示当前字符
// 情况 1 :当前字符不是原因,status 不变
// 情况 2: 当前字符是元音,a ~ u(0 ~ 4),修改相应的状态
// m : 需要修改哪一位的状态,拿到对应的下标索引
m = move(s.charAt(i));
// m != -1 说明遇到元音,修改对应字符的状态
if (m != -1) {
// 异或运算实现改变状态,0 变 1,1 变 0
status ^= (1 << m);
}
// 此时 status 变成 0 ... i 字符串上 a e i o u 的奇偶性
// 找同样的状态最早出现在哪,之前出现过,更新字符串最大长度
if (map[status] != -2) {
ans = Math.max(ans, i - map[status]);
} else {
// 第一次出现,记录当前状态最早出现在 i 位置
map[status] = i;
}
}
return ans;
}
// 返回元音对应的下标索引
public int move(char cha) {
switch (cha) {
case 'a':
return 0;
case 'e':
return 1;
case 'i':
return 2;
case 'o':
return 3;
case 'u':
return 4;
default:
return -1;
}
}
}