知识文档站

Appearance

堆结构和堆排序

堆结构 ​

基本介绍 ​

堆结构是一种特殊的完全二叉树，分为大根堆和小根堆 ​

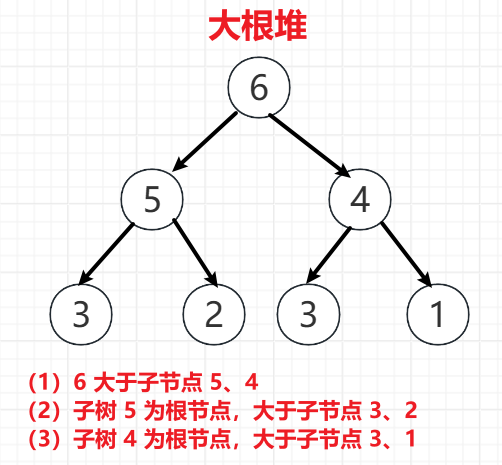
大根堆：任何一颗子树的根节点都大于子节点 ​

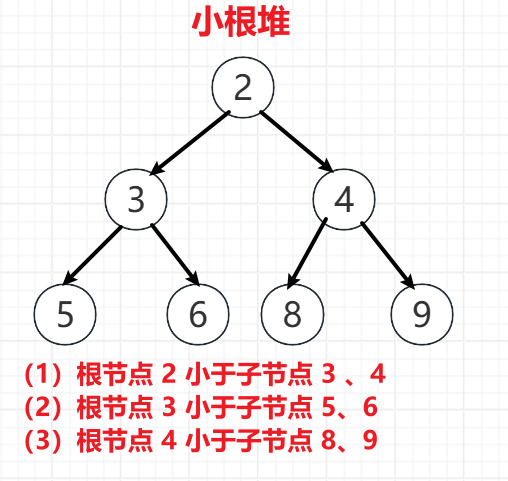
小根堆：任何一颗子树的根节点都小于子节点 ​

以大根堆为例 ​



相关性质 ​

堆结构是一种特殊的完全二叉树，可以用数组实现，通过调整数组中元素的位置，维持堆的结构，用数组的大小 size 来控制堆的大小 ​

堆中元素位置与数组中元素位置的关系：从索引 0 开始，在堆中从上到下，从左到右，依次排列 0 - n-1 位置的元素 ​


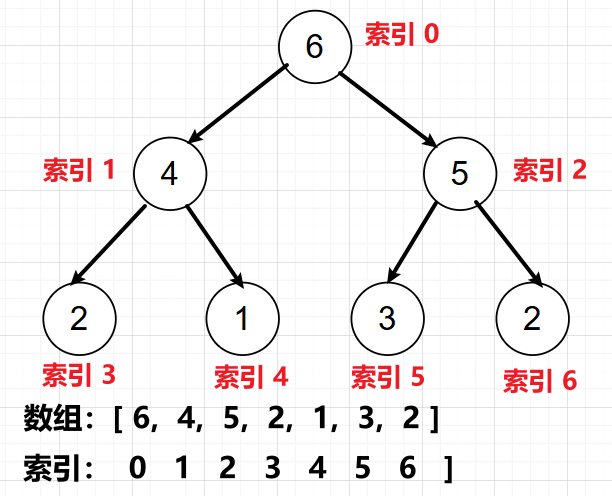
对于任意索引 i 位置的元素，由如下性质 ​

（1）i 的父亲节点：（i - 1） / 2 ​

（2）i 的左孩子：i * 2 + 1 ​

（3）i 的右孩子：i * 2 + 2 ​

堆调整 ​

堆是一种特殊的完全二叉树，n 个节点，树的高度为 log n（以 2 为底） ​

堆的调整过程最差情况是从顶到低，调整的路径怎么也不会大于树的高度，即堆调整的时间复杂度为 O(log n) ​

heapInsert ​

以大根堆为例，这里表示上调整，插入一个元素或者元素变大了，调整堆的结构，维持大根堆的性质 ​

java
// i位置的数，向上调整大根堆
// arr[i] = x，x是新来的！往上看，直到不比父亲大，或者来到 0 位置（顶节点）
public static void heapInsert(int[] arr, int i) {
    // 对于索引 i 位置的元素，其父节点的索引为 (i - 1) / 2
    // 元素交换后，i 来到父节点的位置，继续判断是否需要向上调整
    while (arr[i] > arr[(i - 1) / 2]) {
        swap(arr, i, (i - 1) / 2);
        i = (i - 1) / 2;
    }
}

heapify ​

以大根堆为例，这里表示下调整，删除一个元素或者元素变小了，调整堆的结构，维持大根堆的性质 ​

java
// i位置的数，变小了，又想维持大根堆结构，向下调整大根堆
// 当前堆的大小为size
public static void heapify(int[] arr, int i, int size) {
    int l = i * 2 + 1;
    // 有左孩子
    while (l < size) {
        // 有左孩子，l
        // 右孩子，l + 1
        // 找出左右孩子中最大的孩子下标
        int best = l + 1 < size && arr[l + 1] > arr[l] ? l + 1 : l;
        // 将最大的孩子和当前元素相比，找出最大的元素，并更新最大下标
        best = arr[best] > arr[i] ? best : i;
        // 如果 best == i，说明最强的元素是 i 自己，不需要继续调整
        if (best == i) {
            break;
        }
        swap(arr, best, i);
        i = best;
        l = i * 2 + 1;
    }
}

堆排序 ​

题目链接 ​

https://leetcode.cn/problems/sort-an-array/ ​

思路分析 ​

建立大根堆，将堆顶元素和最后一个元素交换，size--（表示元素排好了，从堆中移除），向下调整堆维持大根堆的结构，依次循环 ​

有两种方式建堆，从顶到底建大根堆，从底到顶建大根堆（时间复杂度为 O（n），推荐使用） ​

堆排序的整体时间复杂度是 O（n * log n） ​

从顶到底建大根堆 ​

堆排序时间复杂度：O(n * log n) ​

构建堆的时间复杂度：O(n * log n) ​

每来一个元素，就 heapInsert 一次，log1 + log2 + log3 + … + logn 收敛于 O(n*logn) ​

java
class Solution {
    public int[] sortArray(int[] nums) {
        if (nums.length > 1) {
            heapSort(nums);
        }
        return nums;
    }

    // 从顶到底建堆
    public void heapSort(int[] arr) {
        int n = arr.length;
        // 建立大根堆
        for (int i = 0; i < n; i++) {
            heapInsert(arr, i);
        }
        // 堆顶元素和最后一个元素交换位置
        int size = n;
        while (size > 0) {
            swap(arr, 0, size - 1);
            size--;
            heapify(arr, 0, size);
        }
    }

    public void heapify(int[] arr, int i, int size) {
        int l = 2 * i + 1;
        // 有左孩子
        while (l < size) {
            // 不一定有右孩子，要判断
            // 找出两个孩子中最大的那个，并记录下标
            int best = l + 1 < size && arr[l + 1] > arr[l] ? l + 1 : l;
            // 将最大的孩子与 i 位置的比较
            best = arr[best] > arr[i] ? best : i;
            // 最大的就是 i 自己，不用调整
            if (best == i) {
                break;
            }
            swap(arr, best, i);
            // 更新 i 位置
            i = best;
            // 继续下一轮的往下调整
            l = 2 * i + 1;
        }

    }

    public void heapInsert(int[] arr, int i) {
        // 维持大根堆的性质
        // 父节点的索引 (i -1) / 2
        while (arr[i] > arr[(i - 1) / 2]) {
            swap(arr, i, (i - 1) / 2);
            i = (i - 1) / 2;
        }
    }

    public void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

从底到顶建大根堆 ​

构建堆的时间复杂度：O(n) ​

堆排序时间复杂度：O(n * log n) ​

从底到顶建大根堆，每加入一个元素就需要往下调整，根据如下对元素的规模分析可以推算建堆的时间复杂度 ​


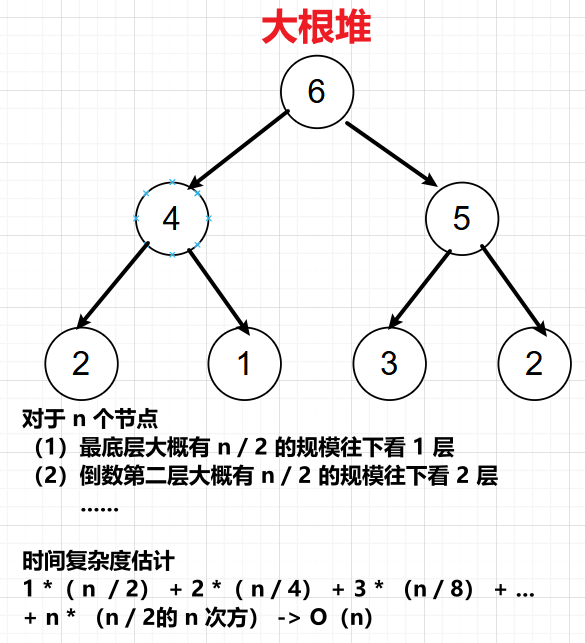
java
class Solution {
    public int[] sortArray(int[] nums) {
        if (nums.length > 1) {
            heapSort(nums);
        }
        return nums;
    }

    // 从低到顶建堆
    public void heapSort(int[] arr) {
        int n = arr.length;
        for (int i = n - 1; i >= 0; i--) {
            heapify(arr, i, n);
        }
        int size = n;
        while (size > 0) {
            swap(arr, 0, size - 1);
            size--;
            heapify(arr, 0, size);
        }
    }

    public void heapify(int[] arr, int i, int size) {
        // 向下调整
        int l = i * 2 + 1;
        while (l < size) {
            // 找出两个孩子中较大的那个
            // 要考虑是否有右孩子
            int best = l + 1 < size && arr[l + 1] > arr[l] ? l + 1 : l;
            // 最大的孩子跟父节点比较
            best = arr[best] > arr[i] ? best : i;
            // 说明最大的节点是自己
            if (best == i) {
                break;
            }
            // 否则就向下调整堆的结构
            swap(arr, i, best);
            // i 来到 best 的位置，继续下一轮的向下调整
            i = best;
            l = i * 2 + 1;
        }
    }

    public void heapInsert(int[] arr, int i) {
        // 向上调整，父节点的索引：(i - 1) / 2
        while (arr[i] > arr[(i - 1) / 2]) {
            swap(arr, i, (i - 1) / 2);
            // i 来到父节点的位置
            i = (i - 1) / 2;
        }
    }

    public void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

⭐ 增倍分析法 ​

Tip

已知以 2 为底的 log 1 + log 2 + log 3 + ... + log n --> O（n * logn） ​

（1）时间复杂度分析 ​

从顶到底建堆，每加入一个元素就要调整堆，而调整堆的时间复杂度是 O(logn)，则堆排序的整体时间复杂度以 2 为底的 log 1 + log 2 + log 3 + ... + log n ​

（2）增倍分析法 ​

n 个数依次进堆，数量级的上限也就是 log n，log n < n * log n，也就是说此时的上限是 n * log n ​

增一倍，2n 个数字的时候，前 n 个数的复杂度如上分析，由于后 n 个数的复杂度是基于前 n 个数的，则后 n 个数的复杂度的规模肯定大于 log n，而已知 n 个数的时候复杂度为 n * log n，也即是说此时的下限是 n * log n ​

对于复杂度来说，只看规模，常熟可以忽略，上限和下限都是 n * log n ​

那复杂度只能是 O（n * log n） ​

Copyright © 2025 Jackson 凌 All Rights Reserved. | 粤ICP备2025441629号-1