前缀树相关题目
接头密钥
题目链接
https://www.nowcoder.com/practice/c552d3b4dfda49ccb883a6371d9a6932
思路分析
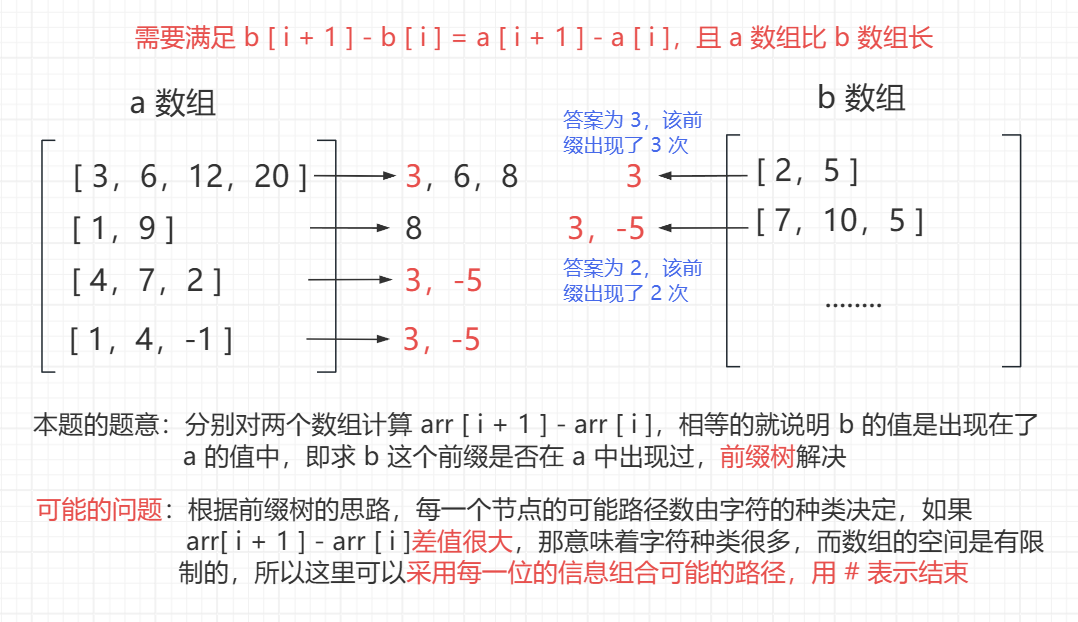
代码实现
java
import java.util.*;
public class Solution {
public static int[] countConsistentKeys(int[][] b, int[][] a) {
build();
StringBuilder builder = new StringBuilder();
// [ 3, 6, 50, 10 ] --> "3#44#-40#"
for (int[] nums : a) {
// 清空内容,但是空间仍然保留
// 下次直接复用,效率高
builder.setLength(0);
for (int i = 1; i < nums.length; i++) {
builder.append(String.valueOf(nums[i] - nums[i - 1]) + "#");
}
insert(builder.toString());
}
int[] ans = new int[b.length];
for (int i = 0; i < b.length; i++) {
builder.setLength(0);
int[] nums = b[i];
for (int j = 1; j < nums.length; j++) {
builder.append(String.valueOf(nums[j] - nums[j - 1]) + "#");
}
ans[i] = prefixNumber(builder.toString());
}
// 使用全局静态空间,为了不影响下一组测试用例
// 的测试结果,需要清空本组测试用例产生的脏数据
clear();
return ans;
}
public static int MAXN = 2000001;
// 数字 0-9 对应下标 0 - 9
// # 符号对应下标 10
// - 符号对应下标 11
public static int[][] tree = new int[MAXN][12];
// 本题只需要求前缀,所以没有使用 end 数组
public static int[] pass = new int[MAXN];
public static int cnt;
public static void build() {
// 节点编号默认从 1 开始
// 0 号位置不用
cnt = 1;
}
public static int path(char cha) {
if (cha == '#') {
return 10;
} else if (cha == '-') {
return 11;
} else {
return cha - '0';
}
}
public static void insert(String word) {
int cur = 1;
pass[cur]++;
for (int i = 0, path; i < word.length(); i++) {
path = path(word.charAt(i));
if (tree[cur][path] == 0) {
tree[cur][path] = ++cnt;
}
cur = tree[cur][path];
pass[cur]++;
}
}
public static int prefixNumber(String pre) {
int cur = 1;
for (int i = 0, path; i < pre.length(); i++) {
path = path(pre.charAt(i));
if (tree[cur][path] == 0) {
return 0;
}
cur = tree[cur][path];
}
return pass[cur];
}
public static void clear() {
for (int i = 1; i <= cnt; i++) {
Arrays.fill(tree[i], 0);
pass[i] = 0;
}
}
}数组中两数最大异或值
题目链接
https://leetcode.cn/problems/maximum-xor-of-two-numbers-in-an-array/description/
思路分析
(1)前缀树实现
异或的性质(1)二进制位不同为 1,相同为 0(2)异或的交换律
异或值需要尽可能大,说明高位的二进制位的异或结果尽可能为 1,那就可以根据该数的二进制位,找到是否有其期望的结果,使得二者异或可以使得该高位的二进制值为 1
⚠️ 注意:题目说的是数都是非负整数,最高位位符号位,非负为 0
假设当前数为 ans(0 0 0 1 0),期望的异或结果是该二进制位置上的值为 1(即 0 1 1 1 1),记为 want,那 ans 需要跟一个数异或的到 want,这个需要得到的数记为 s
ans ^ s = want,根据异或的交换律性质,s = want ^ ans,那就查询是否有 s 这个数,使得 s 的二进制高位跟 ans 异或后可以得到 want,即有没有高位符合要求的前缀,转为前缀树问题
对于每一个数 num,二进制位中的高位为 0 的这些前缀没有意义,放在前缀树中还浪费空间,因此只需要从二进制位中的高位中第一个为 1 的二进制位开始进行异或查询,这样的目的是节省空间
(2)哈希表实现
⭐ 如何保留前面的二进制状态,后面的二进制状态都变为 0 ? ( num >> i ) << i
从高位中第一个二进制状态为 1 的位开始,其后面的位不考虑,都置为 0,运用上面这个技巧
从高位中第一个二进制状态为 1 的位开始往低位讨论,看能否达成期望的目标,思路和前缀树类似,前缀信息转用哈希表存储,如果表里有符合要求的前缀,则说明可以达到期望,更新最大异或结果
这个过程其实就是前缀树中 maxXor 函数的实现过程,前缀信息由前缀树存储转为哈希表存储
哈希表的常数时间会比前缀树更优,所以力扣上哈希表的实现会跑的更快
前缀树实现
java
class Solution {
public static int findMaximumXOR(int[] nums) {
// 根据二进制位来建树
build(nums);
// 本题中,自己可以和自己异或,结果为 0
int ans = 0;
// 遍历每一个数字,maxXor 告诉当前数字,
// 哪个数字跟我异或的值最大,返回
// 不断更新异或的最大值
for (int num : nums) {
ans = Math.max(ans, maxXor(num));
}
// 使用全局静态空间,记得清理脏数据
clear();
return ans;
}
// 准备这么多静态空间就够了,实验出来的
// 如果测试数据升级了规模,就改大这个值
public static int MAXN = 3000001;
// 只关注每个数的二进制状态
public static int[][] tree = new int[MAXN][2];
// 前缀树目前使用了多少空间
public static int cnt;
// 数字只需要从哪一位开始考虑
public static int high;
public static void build(int[] nums) {
cnt = 1;
// 找最大值
int max = Integer.MIN_VALUE;
for (int num : nums) {
max = Math.max(max, num);
}
// 高位为 0 的二进制位无意义
// 无需放到前缀树中,浪费空间
high = 31 - Integer.numberOfLeadingZeros(max);
for (int num : nums) {
insert(num);
}
}
public static void insert(int num) {
int cur = 1;
for (int i = high, path; i >= 0; i--) {
// 记录的是每一位的二进制状态
path = (num >> i) & 1;
if (tree[cur][path] == 0) {
tree[cur][path] = ++cnt;
}
cur = tree[cur][path];
}
}
// 给定一个数 num,返回谁跟 num 异或
// 的值是最大的,将这个最大值返回
public static int maxXor(int num) {
// 最终的异或结果
int ans = 0;
int cur = 1;
for (int i = high, status, want; i >= 0; i--) {
// status :取出第 i 位的状态
status = (num >> i) & 1;
// want :num 第 i 位希望遇到的状态
// 目标 --> status ^ ? = 1
// 根据异或的交换律性质求得 want 的值
want = status ^ 1;
// 查询前缀树中有没有 want 这个希望的状态
// 如果没有,则 want 就是其反面,再异或得到反面
if (tree[cur][want] == 0) {
want ^= 1;
}
// 将结果记录下来,继续检查下一位
ans |= (status ^ want) << i;
cur = tree[cur][want];
}
return ans;
}
public static void clear() {
for (int i = 1; i <= cnt; i++) {
tree[i][0] = 0;
tree[i][1] = 0;
}
}
}哈希表实现
java
class Solution {
public static int findMaximumXOR(int[] nums) {
int max = Integer.MIN_VALUE;
for (int num : nums) {
max = Math.max(num, max);
}
int ans = 0;
HashSet<Integer> set = new HashSet<>();
for (int i = 31 - Integer.numberOfLeadingZeros(max); i >= 0; i--) {
// ans :31 ... i+1 位已达成目标,现在讨论第 i 位是否也可以达成
int want = ans | (1 << i);
// 每次循环讨论一位,讨论前先清空
set.clear();
for (int num : nums) {
// num : 31 .... i,将 i 位置后的二进制位置为 0
// 每次只讨论 i 位置是否能达成期望的目标
num = (num >> i) << i;
set.add(num);
// num ^ ? = want --> ? = want ^ num
if (set.contains(want ^ num)) {
// 如果有想要的期望,更新最大异或值
// 结束该位的讨论,继续讨论下一位
ans = want;
break;
}
}
}
return ans;
}
}二维数组中搜索单词
题目链接
https://leetcode.cn/problems/word-search-ii/
思路分析
本题主要考察剪枝的应用,前缀树可以很好的实现剪枝,同时也可以有很多妙用
(1)指导递归的展开,实现剪枝:判断某个节点是否有必要去搜索,可以查询前缀树中是否有到该节点的路,如果没有,则无需搜索
(2)每个节点增加 String 属性,如果某个节点是字符串的结尾,则将 String 属性不为空,且置为该字符串,方便收集结果,收集完成后置空,再也用不到了
(3)pass 信息剪枝:每次收集节点的时候把节点的 pass 值减少,收集完了返回,沿途的节点的 pass 都更新,当下一次递归时候,发现前缀树中某个节点的 pass 值为 0,不能走,这就说明前面已经收集过了,不能重复收集,这就实现了剪枝
前缀树实现
java
class Solution {
public List<String> findWords(char[][] board, String[] words) {
build(words);
List<String> ans = new ArrayList<>();
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
dfs(board, i, j, 1, ans);
}
}
// 使用全局静态空间,记得清理脏数据
clear();
return ans;
}
// borod : 二维网格
// i,j : 此时来到的格子位置,i 行,j 列
// cur : 前缀树节点的编号,刚来到一个格子的时候还没走过树上的路径,还在节点处
// List<String> ans :收集到了那些字符串,都加入 ans
// 返回值 : 收集到了几个字符串
public static int dfs(char[][] board, int i, int j, int cur, List<String> ans) {
// 越界或者走了回头路,直接返回 0
if (i < 0 || i >= board.length || j < 0 || j >= board[0].length || board[i][j] == 0) {
return 0;
}
// 不越界且不是回头路,记录当前字符
char temp = board[i][j];
// 查询是否有到这个节点的必要
int road = temp - 'a';
cur = tree[cur][road];
// 节点编号从 1 开始
// pass[cur] == 0 说明要么 cur 为 0,要么 cur ≠ 0 但是 pass[cur] == 0
// 可以合并为一句 --> pass[cur] == 0
// if (cur == 0 || pass[cur] == 0) {
// return 0;
// }
if (pass[cur] == 0) {
return 0;
}
// i,j 位置有必要来
// fix : 从当前 i,j 位置出发,一共收集到了几个字符串
int fix = 0;
if (end[cur] != null) {
fix++;
ans.add(end[cur]);
// 收集过了,后面再也用不到了,置空
end[cur] = null;
}
// 把 i,j 位置的字符改成 0,后续的过程是不可以再来到 i,j 位置的
board[i][j] = 0;
fix += dfs(board, i - 1, j, cur, ans);
fix += dfs(board, i + 1, j, cur, ans);
fix += dfs(board, i, j - 1, cur, ans);
fix += dfs(board, i, j + 1, cur, ans);
// 收集过了无需重复收集,这里实现的
pass[cur] -= fix;
// 恢复现场
board[i][j] = temp;
return fix;
}
public static int MAXN = 10001;
public static int[][] tree = new int[MAXN][26];
public static int[] pass = new int[MAXN];
public static String[] end = new String[MAXN];
public static int cnt;
public static void build(String[] words) {
cnt = 1;
for (String word : words) {
// 头节点
int cur = 1;
pass[cur]++;
for (int i = 0, path; i < word.length(); i++) {
path = word.charAt(i) - 'a';
if (tree[cur][path] == 0) {
tree[cur][path] = ++cnt;
}
cur = tree[cur][path];
pass[cur]++;
}
end[cur] = word;
}
}
public static void clear() {
for (int i = 1; i <= cnt; i++) {
Arrays.fill(tree[i], 0);
pass[i] = 0;
end[i] = null;
}
}
}回溯算法实现
java
class Solution {
Set<String> set = new HashSet<>();
List<String> ans = new ArrayList<>();
char[][] grid;
int[][] dirs = new int[][]{{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
boolean[][] visited = new boolean[15][15];
public List<String> findWords(char[][] board, String[] words) {
grid = board;
for (String w : words) {
set.add(w);
}
StringBuilder sb = new StringBuilder();
for (int x = 0; x < grid.length; x++) {
for (int y = 0; y < grid[0].length; y++) {
visited[x][y] = true;
sb.append(grid[x][y]);
dfs(x, y, sb);
visited[x][y] = false;
sb.deleteCharAt(sb.length() - 1);
}
}
return ans;
}
public void dfs(int x, int y, StringBuilder sb) {
// 如果当前爆搜到的字符串长度超过 10,直接剪枝;
if (sb.length() > 10) {
return;
}
// 如果当前搜索到的字符串在 Set 中,则添加到答案
// 同时了防止下一次再搜索到该字符串,需要将该字符串从 Set 中移除
if (set.contains(sb.toString())) {
ans.add(sb.toString());
set.remove(sb.toString());
}
for (int i = 0; i < dirs.length; i++) {
int nextX = x + dirs[i][0];
int nextY = y + dirs[i][1];
// 检验是否越界
if (nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length) {
continue;
}
// 递归条件:下一个点没被访问过
if (!visited[nextX][nextY]) {
visited[nextX][nextY] = true;
sb.append(grid[nextX][nextY]);
dfs(nextX, nextY, sb);
sb.deleteCharAt(sb.length() - 1);
visited[nextX][nextY] = false;
}
}
}
}